min 2x+\(\frac{27}{x^2}\)với x>0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
K
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 7 2021
\(P=2x+\dfrac{27}{x^2}=x+x+\dfrac{27}{x^2}\ge3\sqrt[3]{\dfrac{27x^2}{x^2}}=9\)
\(P_{min}=9\) khi \(x=\dfrac{27}{x^2}\Leftrightarrow x=3\)
8 tháng 7 2019
Với x>0: \(B=x^2+\frac{1}{2x}=x^2+\frac{1}{4x}+\frac{1}{4x}\ge3\sqrt[3]{x^2.\frac{1}{4x}.\frac{1}{4x}}=\frac{3}{2\sqrt[3]{2}}\)(áp dụng bất đẳng thức AM-GM cho ba số)
Dấu '=' xảy ra khi \(x^2=\frac{1}{4x}\Leftrightarrow x^3=\frac{1}{4}\Leftrightarrow x=\frac{1}{\sqrt[3]{4}}.\)(p/s đừng k cho câu trả lời này nhé, mặc dù đúng 100%)
17 tháng 10 2020
Áp dụng trực tiếp bất đẳng thức Cauchy-Schwarz dạng Engel:
\(VT\ge\frac{\left(x+y+z\right)^2}{\left(x+y+z\right)+2\left(x+y+z\right)+3\left(x+y+z\right)}=1\)
Dấu bằng xảy ra khi \(x=y=z=2\)
KN
17 tháng 10 2020
Áp dụng BĐT AM - GM cho 2 số dương, ta được: \(\frac{x^2}{x+2y+3z}+\frac{1}{36}\left(x+2y+3z\right)\ge2\sqrt{\frac{x^2}{x+2y+3z}.\frac{1}{36}\left(x+2y+3z\right)}=\frac{1}{3}x\Rightarrow\frac{x^2}{x+2y+3z}\ge\frac{11}{36}x-\frac{1}{18}y-\frac{1}{12}z\)Tương tự, ta có: \(\frac{y^2}{y+2z+3x}\ge\frac{11}{36}y-\frac{1}{18}z-\frac{1}{12}x\); \(\frac{z^2}{z+2x+3y}\ge\frac{11}{36}z-\frac{1}{18}x-\frac{1}{12}y\)
Cộng theo vế của 3 bất đẳng thức trên, ta được: \(G=\frac{x^2}{x+2y+3z}+\frac{y^2}{y+2z+3x}+\frac{z^2}{z+2x+3y}\ge\frac{1}{6}\left(x+y+z\right)=1\)
Đẳng thức xảy ra khi x = y = z = 2
20 tháng 7 2019
\(1,A=\frac{1}{x^2+y^2}+\frac{1}{xy}=\frac{1}{x^2+y^2}+\frac{1}{2xy}+\frac{1}{2xy}\)
\(\ge\frac{4}{\left(x+y^2\right)}+\frac{1}{\frac{\left(x+y\right)^2}{2}}\ge\frac{4}{1}+\frac{2}{1}=6\)
Dấu "=" <=> x= y = 1/2
20 tháng 7 2019
\(2,A=\frac{x^2+y^2}{xy}=\frac{x}{y}+\frac{y}{x}=\left(\frac{x}{9y}+\frac{y}{x}\right)+\frac{8x}{9y}\ge2\sqrt{\frac{x}{9y}.\frac{y}{x}}+\frac{8.3y}{9y}\)
\(=2\sqrt{\frac{1}{9}}+\frac{8.3}{9}=\frac{10}{3}\)
Dấu "=" <=> x = 3y
PT
7
T
28 tháng 2 2019
=> B = \(\frac{\left(x-1\right)^2+2010}{x^2}=\frac{\left(x-1\right)^2}{x^2}+\frac{2010}{x^2}\)
Vì \(\left(x-1\right)^2\ge0\), \(x^2\)\(\ge\)0 với mọi x
=> để B bé nhất thì \(\frac{2010}{x^2}\)bé nhất
=> \(x^2\) lớn nhất
=> WTF bạn ghi sai đầu bài à ???
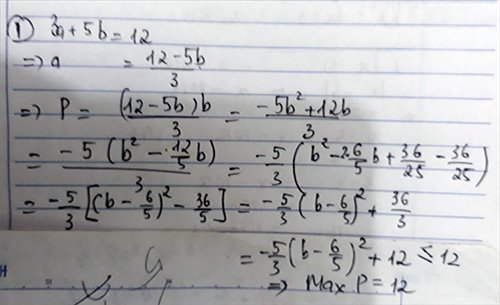
ta có
\(2x+\frac{27}{x^2}=x+x+\frac{27}{x^2}\ge3\sqrt[3]{\frac{x.x.27}{x^2}}=9\)
dấu bằng xảy ra khi \(x=\frac{27}{x^2}\Leftrightarrow x=3\)