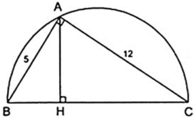
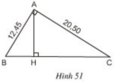
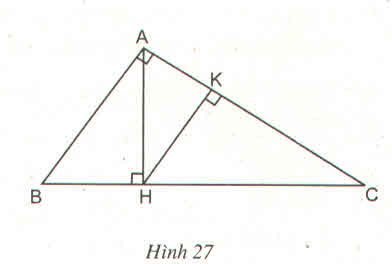
Cho tam giác vuông ABC (góc A= 90 độ), đường cao AH. Tìm tất cả các cặp tam giác đồng dạng với nhau có trong hình và giải thích tại sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 6 2015
2 TG IBA = tg ICA(c-g-c)
2 TG IMA=TG INA(c-g-c) (1)
Các cặp cạnh bằng nhau:
AM=BM vì M là trung điểm của AB
AN=CN vì N là trung điểm của AB
AB=AC vì Tam giác ABC cân.
MI=NI vì (1)
Các góc bằng nhau:
AIB = AIC do AI là đường cao của tam giác ABC.
CBA = BCA vì tam giác ABC cân
IAB=IAC vì tg IBA=ICA
IMA=INA vì (2)
IMB=INC vì góc IMA=INA,mà 2 góc IMB kề bù IMA,INC kề bù INA.
Các góc bằng 90*: BIA và CIA
(cân tại A) vẽ đường cao AH, đường cao BK
Hãy tính độ dài các cạnh của tam giác ABC
và BK, hãy tìm điều kiện của tam giác ABC để tam giác 
là tam giác đều ?
NL
19 tháng 2 2021
a) Vì \(\Delta ABC\) cân tại A, có AH là đường cao
\(\Rightarrow AH\) vừa là đường cao, vừa là đường phân giác của \(\Delta ABC\)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}=\dfrac{\widehat{A}}{2}\)
Xét \(\Delta ABH\) và \(\Delta ACH\) có:
\(\widehat{BAH}=\widehat{CAH}\left(cmt\right)\)
\(\widehat{AHB}=\widehat{AHC}=90^0\)
\(AH\): cạnh chung
\(\Rightarrow\Delta ABH=\Delta ACH\left(ch-gn\right)\)
CM
19 tháng 9 2018
Trong hình bên có 3 cặp tam giác đồng dạng là BHA và BAC; CHA và CAB; HAB và HCA.
CM
30 tháng 9 2018
a) ΔABC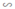 
ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔABC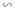 
ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHBA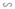 
ΔHAC vì cùng đồng dạng với ΔABC.
b) + ΔABC vuông tại A
⇒ BC2 = AB2 + AC2
(Theo định lý Pytago)
