để tiến tới 30 năm ngày thành lập trường hội cựu học sinh trường Lương thế vinh đã đăng ký một phòng tại trường để găp mặt đại diện các khoá. Lúc đầu phòng có 120 ghế dc xếp thành từng dãy có số ghế t...

TC

TỐNG CÔNG MINH

26 tháng 2 2021 - olm

để tiến tới 30 năm ngày thành lập trường hội cựu học sinh trường Lương thế vinh đã đăng ký một phòng tại trường để găp mặt đại diện các khoá. Lúc đầu phòng có 120 ghế dc xếp thành từng dãy có số ghế trên một dãy như nhau nhưng thực tế phải xếp thêm một dãy và một dãy thêm hai ghế thì mới đủ chỗ cho 156 cựu học sinh vể dự .Hỏi lúc đầu phòng có bao nhiêu dãy và bao nhiêu...

Đọc tiếp

#Toán lớp 9

2

DN

Đỗ Nguyễn Minh Ngọc

26 tháng 2 2021

120 ghế

Đúng(0)

LH

Lê Hùng Kỳ

26 tháng 2 2021

120 cái ghế

Đúng(0)

HM

Hà My

23 tháng 2 2018 - olm

Đây là bài toán giải theo phương trình, các bạn giúp tớ nhé!

Trong phòng hội trường của một trường học có 120 cái ghế và được chia thành các dãy có số ghế bằng nhau. Để chuẩn bị cho cuộc họp, trường trang trí lại phòng họp nên các cô phục vụ đã bớt đi mỗi dãy 4 ghế thì thêm được 5 dãy ghế. Hỏi lúc đầu phòng họp có bao nhiêu dãy ghế?

#Toán lớp 8

2

LK

Lâm Khả Hân

23 tháng 2 2018

gọi dãy ghế lúc đầu là x (đk : x>0, x thuộc Z) thì số dãy ghế sau khi xếp lại là x+5
theo đề bài, ta có :
số ghế mỗi dãy lúc đầu là 120/x
số ghế mỗi dãy sau khi xếp lại là (120/x)-4 / x+5 = 120-4x / x(x+5)
ta có phương trình : 120/x - 4 = 120-4x / x(x+5)
<=> 120-4x / x = 120-4x / x(x+5)
<=> (120-4x)(x+5) / x(x+5) = 120-4x / x(x+5)
<=> (120-4x)(x+5)=120-4x
<=> (120-4x)(x+5) - (120-4x) = 0
<=> (120-4x)(x+5-1) = 0
<=> (120-4x)(x+4) = 0
<=> 120-4x = 0
x+4 =0
<=> x = 30 (thỏa đk)
x = -4 (ko thỏa đk)
vậy số dãy ghế ban đầu là 30

Đúng(0)

AD

Âu Dương Khắc

23 tháng 2 2018

120 cái ghế

Đúng(0)

LT

Lê Thụy Sĩ

31 tháng 5 2019 - olm

Một trường học tổ chức buổi lễ tri ân cho học sinh khối 9. Lúc đầu hội trường có 210 ghế xếp thành từng dãy , mỗi dãy có số ghế như nhau. Nhưng thực tế phải xếp thêm 2 dãy ghế và mỗi dãy thêm 2 ghế thì mới đủ chỗ cho 272 học sinh. Hỏi lúc đầu hội trường có bao nhiêu dãy ghế và mỗi dãy có bao nhiêu ghế?

AI GIẢI VỚI HUHU !!!!

#Toán lớp 9

1

DH

Đặng Hoàng Phúc

31 tháng 5 2019

MÌNH GIẢI SAI MONG CÁC BẠN THÔNG CẢM VÀ SỬA JUP MIK!!

Gọi số dãy ghế lúc đầu là x (dãy ghế) Đk: x>2

Số ghế mỗi dãy lúc đầu là 210/x(ghế)

dãy ghế lúc sau là x+2(dãy ghế)

Số ghế mỗi dãy lúc sau là 272/x+2(ghế)

Vì thực tế phải xếp thêm mỗi dãy 2 ghế nên ta có pt:

(210/x)-(272/x+2)+2=0(1)

Giải pt (1) ta có: x₁=15(TM),x₂=14(TM)

Với số dãy ghế lúc đầu là 15 (dãy) suy ra mỗi dãy có số ghế là 14 (ghế)

Với số dãy ghế lúc đầu là 14 (dãy) suy ra mỗi dãy có số ghế là 15 (ghế)

Đúng(0)

HV

Hoàng Việt Đức Anh

28 tháng 1 2018 - olm

Các bạn giúp mình câu này nha mình cảm ơn các bạn !À mà nó hơi khó một tí đấy nha các bạn (đề nâng cao lớp 8 đó các bạn ạ !) Trong phòng hội trường của một trường học có 120 cái ghế và được chia thành các dãy ghế bằng nhau. Để chuẩn bị cho cuộc họp, trường trang trí lại phòng họp nên các cô phục vụ đã bớt đi mỗi dãy 4 ghế thì được 5 dãy ghế. Hỏi ban đầu trong phòng họp...

Đọc tiếp

#Toán lớp 8

2

TH

ʚTrần Hòa Bìnhɞ

28 tháng 1 2018

120 cái ghế

Đúng(0)

HV

Hoàng Việt Đức Anh

28 tháng 1 2018

số dãy ghế bạn ơi

Đúng(0)

TN

Thien Nguyen

17 tháng 5 2021

Hội trường của nhà trường có 350 ghế ngồi được sắp xếp thành 1 số dãy ghế mà số ghế của mỗi dãy đều bằng nhau, mỗi ghế chỉ một người ngồi; trong lễ khen thưởng học sinh giỏi có 300 học sinh và đại biểu tham dự nên hội trường sắp xếp giảm 5 dãy ghế và mỗi dãy ghế còn lại đều sắp xếp tăng thêm 1 ghế. Hỏi ban đầu có bao nhiêu dãy ghế và mỗi dãy ghế có bao nhiêu...

Đọc tiếp

#Toán lớp 9

0

KK

Kim Khánh Linh

18 tháng 5 2021 - olm

1) Hội trường của nhà trường có $350$ ghế ngồi được sắp xếp thành một số dãy ghế mà số ghế của mỗi dãy đều bằng nhau, mỗi ghế chỉ một người ngồi; trong lễ khen thưởng học sinh giỏi có $300$ học sinh và đại biểu tham dự nên hội trường sắp xếp giảm $5$ dãy ghế và mỗi dãy ghế còn lại đều sắp xếp tăng thêm $1$ ghế. Hỏi ban đầu hội trường có bao nhiêu dãy ghế và mỗi...

Đọc tiếp

#Toán lớp 9

1

TD

Trịnh Đăng Khoa

3 tháng 4 2022

Đúng(0)

NT

Nguyễn Tú Linh

9 tháng 4 2017 - olm

Trong một phòng họp có 360 ghế xếp thành các dãy và số ghế mỗi dãy bằng nhau, có một lần phòng họp xếp thêm một dãy ghế và mỗi dãy tăng thêm một ghế (số ghế trong dãy vẫn bằng nhau) để đủ chỗ cho 400 học sinh ngồi. Hỏi bình thường tronh phòng học có bao nhiêu dãy ghế?

#Toán lớp 9

0

MK

mr karik 2005

2 tháng 2 2019 - olm

Một hội trường có 500 ghế ngồi, người ta xếp chúng thành các dãy có số ghế như nhau. Nếu mỗi dãy có thêm 3 ghế và bớt đi 3 dãy thì số ghế trong hội trường vẫn phải bổ sung thêm 6 chiếc. Hỏi lúc đầu người ta định xếp bao nhiêu dãy ghế?

#Toán lớp 8

1

VA

Việt Anh

2 tháng 2 2019

Giả sử hội trường có a dãy và b là số ghế của mỗi dãy. (a,b∈N∗a,b∈N∗).

Ta có phương trình: ab=500ab=500 và

⇒(a−3)(b+3)=506⇒ab−3b+3a−9=506⇒3(a−b)=15⇒a−b=5⇒a(a−5)=500⇔a=25⇒(a−3)(b+3)=506⇒ab−3b+3a−9=506⇒3(a−b)=15⇒a−b=5⇒a(a−5)=500⇔a=25

Vậy lúc đầu người ta định xếp 2525 dãy ghế.

Đúng(1)

PT

Pham Trong Bach

26 tháng 6 2017

Trong một phòng họp có 360 ghế được xếp thành các dãy và số ghế trong mỗi dãy đều bằng nhau. Có một lần phòng họp phải xếp thêm một dãy ghế và mỗi dãy tăng một ghế (số ghế trong các dãy vẫn bằng nhau) để đủ chỗ cho 400 đại biểu. Hỏi bình thường trong phòng có bao nhiêu dãy ghế?

#Toán lớp 9

1

CM

Cao Minh Tâm

26 tháng 6 2017

Gọi x (dãy) là số dãy ghế ban đầu của phòng họp.

Điều kiện: x ∈N*

Khi đó số ghế ngồi trong một dãy là: 360/x (ghế)

số dãy ghế sau khi tăng là x + 1 (dãy)

số ghế ngồi trong một dãy sau khi tăng là: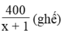 Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Theo đề bài, ta có phương trình:

⇔ 400x – 360(x + 1) = x(x + 1)

⇔ 400x – 360x – 360 = x 2 + x ⇔ x 2 – 39x + 360 = 0

∆ = - 39 2 – 4.1.360 = 1521 – 1440 = 81 > 0

∆ = 81 = 9

Cả hai giá trị của x đều thỏa mãn điều kiện bài toán.

Vậy bình thường trong phòng có 15 hoặc 24 dãy ghế.

Đúng(0)

SG

Sách Giáo Khoa

8 tháng 5 2017

Trong một phòng họp có 360 ghế được xếp thành các dãy và số ghế trong mỗi dãy đều bằng nhau. Có một lần phòng họp phải xếp thêm một dãy ghế và mỗi dãy ghế tăng 1 ghế (số ghế trong các dãy bằng nhau) để đủ chỗ cho 400 đại biểu. Hỏi bình thường trong phòng có bao nhiêu dãy ghế ?

#Toán lớp 9

1

NT

Nguyen Thuy Hoa

21 tháng 6 2017

Hàm số y = ax^2 (a khác 0). Phương trình bậc hai một ẩn

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP