Giải chi tiết câu b giúp em với ạ. Đề bài bảo tìm n nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x=\left(\dfrac{1}{2}\right)^3:\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}\right)^{3-1}=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
đề: tìm 2 số a và b biết
a+b=5 và 2a-b=4
mọi người giải giúp mình với ạ kém theo lời giải chi tiết nha

Ta có: \(a+b=5\Rightarrow a=5-b\)
Thay \(a=5-b\) vào \(2a-b=4\) ta có:
\(2\cdot\left(5-b\right)-b\)
\(\Rightarrow10-2b-b=4\)
\(\Rightarrow10-3b=4\)
\(\Rightarrow3b=10-4\)
\(\Rightarrow3b=6\)
\(\Rightarrow b=\dfrac{6}{3}=2\)
Lúc này ta tìm được \(a\):
\(a=5-b=5-2=3\)
Vậy: \(a=3,b=2\)

10.
\(H\left(x\right)=-5x^4+10x^3-15x+1\)
\(=-5x\left(x^3-2x^2+3\right)+1\)
\(=-5x.0+1\)
\(=1\)
9.
\(P\left(x\right)-Q\left(x\right)=\left(1-a\right)x^3+x^2+x-6\)
\(P\left(x\right)-Q\left(x\right)\) là đa thức bậc 3 khi và chỉ khi \(1-a\ne0\)
\(\Rightarrow a\ne1\)

Bài 2:
b: Ta có: \(B=\dfrac{15-5\sqrt{x}}{x-5\sqrt{x}+6}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{-5\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}-2}=1\)

\(b,\widehat{K_1}=\widehat{KNQ}+\widehat{NQK}=41+90=131\left(góc.ngoài\right)\)
\(d,NH\perp PQ;PQ//NK\Rightarrow NH\perp NK\Rightarrow\widehat{HNK}=90\)
\(\widehat{NKQ}=180-\widehat{K_1}=180-131=49\)
\(\widehat{HAQ}=180-\widehat{HNK}-\widehat{NKQ}=180-90-49=41\)

\(lim\left(\sqrt[3]{n^3+4}-\sqrt[3]{n^3-1}\right)\)
\(=lim\left(\sqrt[3]{1+\dfrac{4}{n^3}}-\sqrt[3]{1-\dfrac{1}{n^3}}\right)=\sqrt[3]{1}-\sqrt[3]{1}=0\)
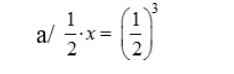 giúp em bài này với ạ,giải chi tiết luôn nha,em cảm ơn
giúp em bài này với ạ,giải chi tiết luôn nha,em cảm ơn




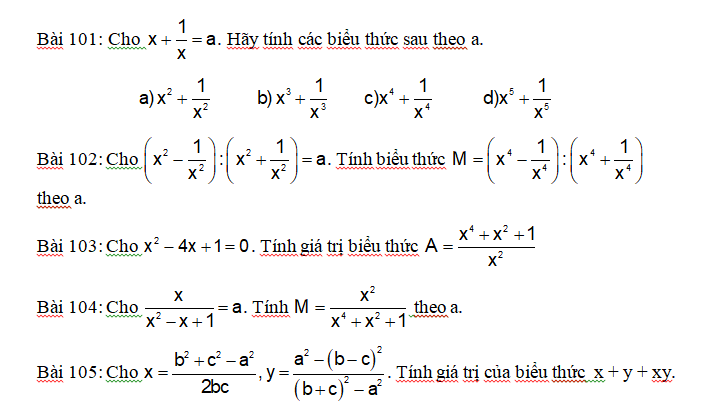

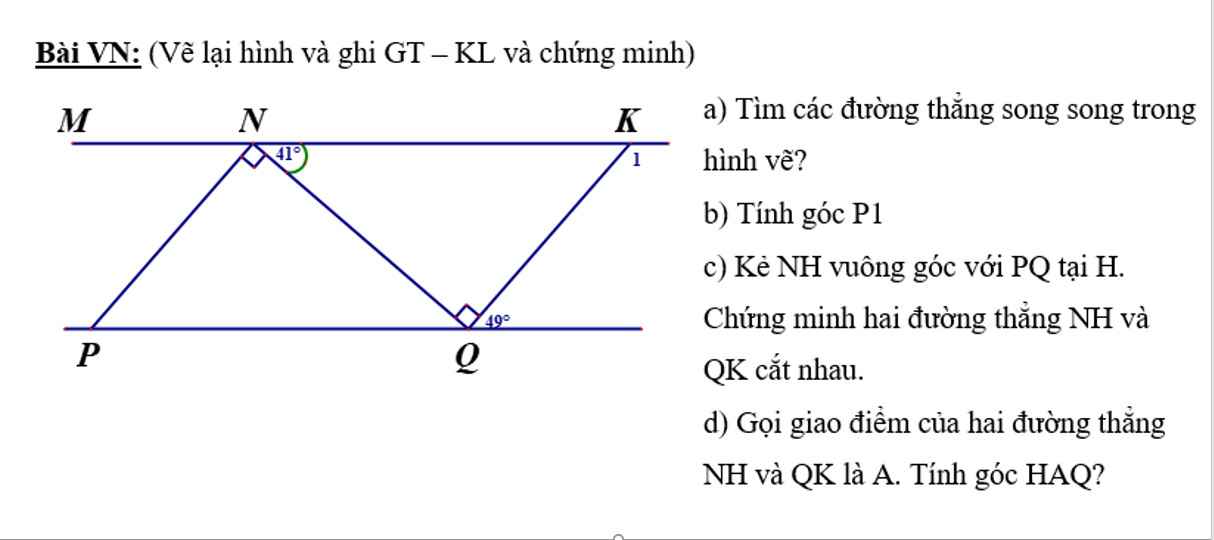 ĐỀ BÀI CÂU B LÀ TÍNH GÓC K1 ; không phải là P1 nhé
ĐỀ BÀI CÂU B LÀ TÍNH GÓC K1 ; không phải là P1 nhé
a, \(u_n=u_1.q^{n-1}\)
\(\Leftrightarrow192=u_1.2^n\)
\(\Leftrightarrow u_1=\dfrac{192}{2^n}\)
\(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}\)
\(\Leftrightarrow189=\dfrac{\dfrac{192}{2^n}\left(1-2^n\right)}{1-2}\)
\(\Leftrightarrow189=192-\dfrac{192}{2^n}\)
\(\Leftrightarrow\dfrac{192}{2^n}=3\)
\(\Leftrightarrow2^n=2^6\)
\(\Rightarrow n=6\)