Cách tìm phương trình đường trung trực của đoạn thẳng AB với A(x1;y1) và B(x2;y2)?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
1
CM
6 tháng 8 2017
- Vẽ đoạn thẳng AB = 24mm
- Vẽ trung điểm I cuả AB
Vì I là trung điểm của AB nên IA = IB = AB/2 = 12 (mm)
Đặt thước thẳng trùng với đường thẳng AB sao cho vạch 0 trùng với điểm A , vạch 12 cho ta vị trí điểm I.
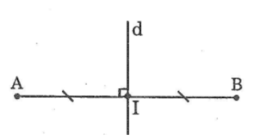
- Vẽ đường thẳng d đi qua I và d⊥ AB
Đặt êke sao cho một cạnh góc vuông của êke trùng với đường thẳng AB, đỉnh góc vuông của êke trùng với I, vẽ đường thẳng đi qua cạnh góc vuông còn lại của êke ta được đường thẳng d.
Khi đó d là trung trực của AB.
Y
0
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
\(\overrightarrow{AB}=\left(4;4\right)=4\left(1;1\right)\)
Đường trung trực của AB vuông góc AB nên nhận \(\left(1;-1\right)\) là 1 vtcp
Gọi M là trung điểm AB \(\Rightarrow M\left(1;3\right)\)
Phương trình trung trực AB qua M có dạng: \(\left\{{}\begin{matrix}x=1+t\\y=3-t\end{matrix}\right.\)
CM
11 tháng 8 2017
Gọi M trung điểm của AB nên M( 2; 1)
Ta có 
Gọi d là đường thẳng trung trực của AB
thì d qua M(2; 1) và nhận 
làm VTPT.
Phương trình đường thẳng d là:
1( x- 2) – 6.(y -1) =0
Hay x- 6y+ 4= 0.
Chọn D