Cho phương trình: (x−1)(x2−2mx+m2−2m+2)=0(x−1)(x2−2mx+m2−2m+2)=0 (1)
Giá trị m nguyên nhỏ nhất để phương trình (1) có 3 nghiệm phân biệt là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 11 2021
\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)
14 tháng 5 2023
Δ=(2m)^2-4(m^2+2m+3)
=4m^2-4m^2-8m-12=-8m-12
Để PT có 2 nghiệm pb thì -8m-12>0
=>-8m>12
=>m<-3/2
x1^3+x2^3=108
=>(x1+x2)^3-3x1x2(x1+x2)=108
=>(-2m)^3-3(m^2+2m+3)*(-2m)=108
=>-8m^3+6m(m^2+2m+3)=108
=>-8m^3+6m^3+12m^2+18m-108=0
=>-2m^3+12m^2+18m-108=0
=>-2m^2(m-6)+18(m-6)=0
=>(m-6)(-2m^2+18)=0
=>m=-3
4 tháng 8 2017
1.Ta có \(\Delta=4m^2-4\left(m^2-m-3\right)=4m+12\)
Để phương trình có 2 nghiệm phân biệt \(\Rightarrow\Delta>0\Rightarrow4m+12>0\Rightarrow m>-3\)
Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=2m\\x_1.x_2=m^2-m-3\end{cases}}\)
a. Phương trình có 2 nghiệm trái dấu \(\Rightarrow x_1.x_2< 0\Rightarrow m^2-m-3< 0\Rightarrow\frac{1-\sqrt{13}}{2}< m< \frac{1+\sqrt{13}}{2}\)
Vậy \(\frac{1-\sqrt{13}}{2}< m< \frac{1+\sqrt{13}}{2}\)
b. Phương trình có 2 nghiệm phân biệt dương \(\Leftrightarrow\hept{\begin{cases}x_1+x_2=2m>0\\x_1.x_2=m^2-m-3>0\end{cases}\Leftrightarrow\hept{\begin{cases}m>0\\m< \frac{1-\sqrt{13}}{2}\end{cases}\left(l\right);\hept{\begin{cases}m>0\\m>\frac{1+\sqrt{13}}{2}\end{cases}\Leftrightarrow m>\frac{1+\sqrt{13}}{2}}}}\)
Vậy \(m>\frac{1+\sqrt{13}}{2}\)
2. a.Ta có \(\Delta=\left(2m-1\right)^2+4m=4m^2-4m+1+4m=4m^2+1\)
Ta thấy \(\Delta=4m^2+1>0\forall m\)
Vậy phương trình luôn có 2 nghiejm phân biệt với mọi m
b. Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=1-2m\\x_1.x_2=-m\end{cases}}\)
Để \(x_1-x_2=1\Leftrightarrow\left(x_1-x_2\right)^2=1\Leftrightarrow\left(x_1+x2\right)^2-4x_1x_2=1\)
\(\Leftrightarrow\left(1-2m\right)^2-4.\left(-m\right)=1\Leftrightarrow4m^2-4m+1+4m=1\)
\(\Leftrightarrow m^2=0\Leftrightarrow m=0\)
Vậy \(m=0\)thoă mãn yêu cầu bài toán
XO
2 tháng 5 2023
Phương trình đã cho có nghiệm phân biệt khi :
\(\Delta'=m^2-\left(m^2+2m+3\right)=-2m-3>0\)
\(\Leftrightarrow m< -\dfrac{3}{2}\)(*)
Hệ thức Viette : \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=m^2+2m+3\end{matrix}\right.\)
Có \(x_1^3+x_2^3=108\)
\(\Leftrightarrow\left(x_1+x_2\right).\left(x_1^2-x_1x_2+x_2^2\right)=108\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=108\)
\(\Leftrightarrow-8m^3+6m\left(m^2+2m+3\right)=108\)
\(\Leftrightarrow m^3-6m^2-9m+54=0\)
\(\Leftrightarrow\left(m-6\right).\left(m-3\right).\left(m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=6\\m=\pm3\end{matrix}\right.\)
Kết hợp (*) được m = -3 thỏa mãn
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2021
\(\Delta'=m^2+2m+6=\left(m+1\right)^2+5>0\) ;\(\forall m\Rightarrow\) pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=-2m-6\end{matrix}\right.\)
Đặt \(P=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(P=\left(-2m\right)^2-2\left(-2m-6\right)=4m^2+4m+12\)
\(P=\left(2m+1\right)^2+11\ge11\)
\(P_{min}=11\) khi \(m=-\dfrac{1}{2}\)
CM
8 tháng 5 2019
PT x 2 − 2 m + 1 x + m 2 − 1 = 0 ( 1 ) có 2 nghiệm phân biệt x 1 , x 2
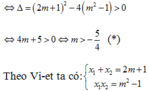
Theo Vi-et ta có: x 1 + x 2 = 2 m + 1 x 1 x 2 = m 2 − 1
Ta có: x 1 2 + x 2 2 + 8 x 1 x 2 = x 1 + x 2 2 + 6 x 1 x 2 = 2 m + 1 2 + 6 m 2 − 1
= 10 m 2 + 2 5 m + 1 25 − 27 5 = 10 m + 1 5 2 − 27 5
⇒ x 1 2 + x 2 2 + 8 x 1 x 2 ≥ − 27 5
Dấu ‘=’ xảy ra khi m = − 1 5 (thỏa mãn (*))
Vậy x 1 2 + x 2 2 + 8 x 1 x 2 đạt giá trị nhỏ nhất khi m = − 1 5
Đáp án cần chọn là: C
bài này sử dụng định lí vi-ét nha