Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.Ta có \(\Delta=4m^2-4\left(m^2-m-3\right)=4m+12\)
Để phương trình có 2 nghiệm phân biệt \(\Rightarrow\Delta>0\Rightarrow4m+12>0\Rightarrow m>-3\)
Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=2m\\x_1.x_2=m^2-m-3\end{cases}}\)
a. Phương trình có 2 nghiệm trái dấu \(\Rightarrow x_1.x_2< 0\Rightarrow m^2-m-3< 0\Rightarrow\frac{1-\sqrt{13}}{2}< m< \frac{1+\sqrt{13}}{2}\)
Vậy \(\frac{1-\sqrt{13}}{2}< m< \frac{1+\sqrt{13}}{2}\)
b. Phương trình có 2 nghiệm phân biệt dương \(\Leftrightarrow\hept{\begin{cases}x_1+x_2=2m>0\\x_1.x_2=m^2-m-3>0\end{cases}\Leftrightarrow\hept{\begin{cases}m>0\\m< \frac{1-\sqrt{13}}{2}\end{cases}\left(l\right);\hept{\begin{cases}m>0\\m>\frac{1+\sqrt{13}}{2}\end{cases}\Leftrightarrow m>\frac{1+\sqrt{13}}{2}}}}\)
Vậy \(m>\frac{1+\sqrt{13}}{2}\)
2. a.Ta có \(\Delta=\left(2m-1\right)^2+4m=4m^2-4m+1+4m=4m^2+1\)
Ta thấy \(\Delta=4m^2+1>0\forall m\)
Vậy phương trình luôn có 2 nghiejm phân biệt với mọi m
b. Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=1-2m\\x_1.x_2=-m\end{cases}}\)
Để \(x_1-x_2=1\Leftrightarrow\left(x_1-x_2\right)^2=1\Leftrightarrow\left(x_1+x2\right)^2-4x_1x_2=1\)
\(\Leftrightarrow\left(1-2m\right)^2-4.\left(-m\right)=1\Leftrightarrow4m^2-4m+1+4m=1\)
\(\Leftrightarrow m^2=0\Leftrightarrow m=0\)
Vậy \(m=0\)thoă mãn yêu cầu bài toán

Δ=(2m)^2-4(m^2+2m+3)
=4m^2-4m^2-8m-12=-8m-12
Để PT có 2 nghiệm pb thì -8m-12>0
=>-8m>12
=>m<-3/2
x1^3+x2^3=108
=>(x1+x2)^3-3x1x2(x1+x2)=108
=>(-2m)^3-3(m^2+2m+3)*(-2m)=108
=>-8m^3+6m(m^2+2m+3)=108
=>-8m^3+6m^3+12m^2+18m-108=0
=>-2m^3+12m^2+18m-108=0
=>-2m^2(m-6)+18(m-6)=0
=>(m-6)(-2m^2+18)=0
=>m=-3

Phương trình đã cho có nghiệm phân biệt khi :
\(\Delta'=m^2-\left(m^2+2m+3\right)=-2m-3>0\)
\(\Leftrightarrow m< -\dfrac{3}{2}\)(*)
Hệ thức Viette : \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=m^2+2m+3\end{matrix}\right.\)
Có \(x_1^3+x_2^3=108\)
\(\Leftrightarrow\left(x_1+x_2\right).\left(x_1^2-x_1x_2+x_2^2\right)=108\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=108\)
\(\Leftrightarrow-8m^3+6m\left(m^2+2m+3\right)=108\)
\(\Leftrightarrow m^3-6m^2-9m+54=0\)
\(\Leftrightarrow\left(m-6\right).\left(m-3\right).\left(m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=6\\m=\pm3\end{matrix}\right.\)
Kết hợp (*) được m = -3 thỏa mãn

\(\Delta'=m^2+2m+6=\left(m+1\right)^2+5>0\) ;\(\forall m\Rightarrow\) pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=-2m-6\end{matrix}\right.\)
Đặt \(P=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(P=\left(-2m\right)^2-2\left(-2m-6\right)=4m^2+4m+12\)
\(P=\left(2m+1\right)^2+11\ge11\)
\(P_{min}=11\) khi \(m=-\dfrac{1}{2}\)

a) Xét pt đã cho có \(a=m^2+m+1\); \(b=-\left(m^2+2m+2\right)\); \(c=-1\)
Nhận thấy rằng \(ac=\left(m^2+m+1\right)\left(-1\right)=-\left(m^2+m+1\right)\)
\(=-\left(m^2+2m.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\right)=-\left(m+\dfrac{1}{2}\right)^2-\dfrac{3}{4}\)
Vì \(-\left(m+\dfrac{1}{2}\right)^2\le0\) và \(-\dfrac{3}{4}< 0\) nên \(-\left(m+\dfrac{1}{2}\right)^2-\dfrac{3}{4}< 0\) hay \(ac< 0\). Vậy pt đã cho luôn có 2 nghiệm trái dấu.
b) Theo câu a, ta đã chứng minh được pt đã cho luôn có 2 nghiệm trái dấu \(x_1,x_2\).
Áp dụng hệ thức Vi-ét, ta có \(S=x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m^2+2m+2\right)}{m^2+m+1}=\dfrac{m^2+2m+2}{m^2+m+1}\)
Nhận thấy \(m^2+m+1\ne0\) nên ta có:
\(\left(m^2+m+1\right)S=m^2+2m+2\) \(\Leftrightarrow Sm^2+Sm+S-m^2-2m-2=0\)\(\Leftrightarrow\left(S-1\right)m^2+\left(S-2\right)m+\left(S-2\right)=0\)(*)
pt (*) có \(\Delta=\left(S-2\right)^2-4\left(S-1\right)\left(S-2\right)\)\(=S^2-4S+4-4\left(S^2-3S+2\right)\)\(=S^2-4S+4-4S^2+12S-8\)\(=-3S^2+8S-4\)
Để pt (*) có nghiệm thì \(\Delta\ge0\) hay \(-3S^2+8S-4\ge0\)\(\Leftrightarrow-3S^2+6S+2S-4\ge0\)\(\Leftrightarrow-3S\left(S-2\right)+2\left(S-2\right)\ge0\) \(\Leftrightarrow\left(S-2\right)\left(2-3S\right)\ge0\)
Ta xét 2 trường hợp:
TH1: \(\left\{{}\begin{matrix}S-2\ge0\\2-3S\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S\ge2\\S\le\dfrac{2}{3}\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}S-2\le0\\2-3S\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S\le2\\S\ge\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\dfrac{2}{3}\le S\le2\) (nhận)
Khi \(S=\dfrac{2}{3}\) thì (*) \(\Leftrightarrow\left(\dfrac{2}{3}-1\right)m^2+\left(\dfrac{2}{3}-2\right)m+\dfrac{2}{3}-2=0\)\(\Leftrightarrow-\dfrac{1}{3}m^2-\dfrac{4}{3}m-\dfrac{4}{3}=0\)\(\Leftrightarrow m^2+4m+4=0\)
\(\Leftrightarrow\left(m+2\right)^2=0\) \(\Leftrightarrow m+2=0\) \(\Leftrightarrow m=-2\)
Khi \(S=2\) thì (*) \(\Leftrightarrow\left(2-1\right)m^2+\left(2-2\right)m+2-2=0\)\(\Leftrightarrow m^2=0\)
\(\Leftrightarrow m=0\)
Vậy GTNN của S là \(\dfrac{2}{3}\) khi \(m=-2\) và GTLN của S là \(2\) khi \(m=0\)
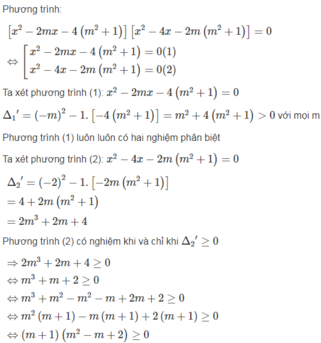






bài này sử dụng định lí vi-ét nha