Bài 5: Cho ABC, M là trung diêm cüa BC. Trên tia dôi cüa tia MA lây diêm D sao cho MD — MA. Tù D vê tia DxL BC tai E. Trên tia DX lây diêm K sao cho E là trung diêm cùa DK. Chfrng minh râng: a) AAMC...

TK

Trần Khánh Ngọc

15 tháng 12 2021 - olm

Bài 5: Cho ABC, M là trung diêm cüa BC. Trên tia dôi cüa tia MA lây diêm D sao cho MD — MA. Tù D vê tia DxL BC tai E. Trên tia DX lây diêm K sao cho E là trung diêm cùa DK. Chfrng minh râng: a) AAMC - ADMB. b) AC//BD. c) MA - MK. d) AK//BC. Bài 6: Cho AABC, D là trung diêm cüa AB, E là trung diêm cüa AC.Vë diêm F sao cho E là trung diêm cua DF. Chûng minh râng: a) DB - CF. b) ABDC = AFCD. 1 c) DE//BC;DE = -BC....

Đọc tiếp

#Toán lớp 7

0

PK

Phạm Khánh Huyền

3 tháng 8 2015 - olm

Cho tam giác ABC , M là trung điểm cạnh BC , trên tia đối của tia MA lấy điểm D sao cho MA=MD .Từ D vẽ tia Dx vuông góc BC tại E .Trên tia Dx lấy điểm K sao cho E là trung điểm của DK .Chứng minh :

a) AC//BD

b)MA=MK

c)AK//BC

#Toán lớp 7

0

TN

Trang Nguyễn

11 tháng 1 2019 - olm

Cho tam giác ABC , M là trung điểm cạnh BC , trên tia đối của tia MA lấy điểm D sao cho MA=MD .Từ D vẽ tia Dx vuông góc BC tại E .Trên tia Dx lấy điểm K sao cho E là trung điểm của DK .Chứng minh :

a) AC//BD

b)MA=MK

c,AK//BC

#Toán lớp 7

0

DM

Do minh linh trang

22 tháng 11 2019 - olm

cho tam giác ABC ,M là triung điểm củt BC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA . Từ D vẽ tia Dx vuông góc với BC tại E. Trên tia Dx lấy điểm K sao cho E là trung điểm của DK . CMR

a) Tam giác AMC=tam giác DMB

b) AC// BD

c)MA = MK

d) AK//BC

#Toán lớp 7

0

BN

Bùi Ngọc Tố Uyên

4 tháng 12 2021

Bài 11: Cho △ABC, lấy M là trung điểm cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD. Chứng minh rằng:a) △AMB = △DMCb) AC // BDc) Kẻ AH ⏊ BC, DK⏊ BC( H,K thuộc BC). Chứng minh BK = CHd) Gọi I là trung điểm của AC, vẽ điểm E sao cho I là trung điểm của BE. Chứng minh C là trung điểm DE.Mong mn làm giúp mik bài này mik cảm...

Đọc tiếp

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

4 tháng 12 2021

Bài 11:

b: Xét tứ giác ABDC có

M là trung điểm của AD

M là trung điểm của BC

Do đó: ABDC là hình bình hành

Suy ra: AC//BD

Đúng(0)

PN

Padparascha Nguyen

27 tháng 11 2017 - olm

Cho \(\Delta ABC\)có AB<AC. M là trung điểm cạnh BC. Trên tia đối tia MA lấy điểm D sao cho MA=MD. Từ A vẽ tia\(Ax\perp BC\)tại E, trên tia đối của Ax lấy điểm K sao cho E là trung điểm của AK. Chứng minh rằng \(DK\perp Ax\)

#Toán lớp 7

0

NK

Nguyễn Khánh Ngọc

28 tháng 12 2023 - olm

Bài 3. (3,0 điểm) Cho tam giác ABC, lấy M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD. a) Chứng minh Δ∆AMB = Δ∆DMC; b) Chứng minh AC // BD; c) Kẻ AH ⊥ BC, DK ⊥ BC (H, K thuộc BC). Chứng minh BK = CH; d) Gọi I là trung điểm của AC, vẽ điểm E sao cho I là trung điểm của BE. Chứng minh C là trung điểm của...

Đọc tiếp

#Toán lớp 7

0

MD

mạnh dũng hà

11 tháng 12 2015 - olm

Cho tam giác ABC có AB < AC. Trên BC lấy M sao cho MB = MC. Trên tia đối của tia MA lấy D sao cho MA = MD.

Từ A hạ AH vuông góc với BC tại H. Trên tia đối của HA lấy điểm E sao cho H là trung điểm AE. Cho K là trung điểm ED.

Chứng minh KM vuông góc BC.

#Toán lớp 7

0

AA

Anh'ss Anh'ss

10 tháng 12 2020

Cho ∆ABC. Gọi M là trung điểm của cạnh BC, trên tia đối của tia MA lấy điểm D sao cho MA = MD.

a) Chứng minh ∆AMB = ∆DMC;

b) BD // AC;

c)Gọi N là trung điểm của AB, trên tia đối của tia NC lấy điểm E sao cho NE = NC. Chứng minh B là trung điểm của DE.

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

7 tháng 10 2023

a: Xét ΔAMB và ΔDMC có

MA=MD

góc AMB=góc DMC

MB=MC

Do đó: ΔAMB=ΔDMC

b: Xét tứ giác ABDC có

M là trung điểm chung của AD và BC

Do đó: ABDC là hình bình hành

=>BD//AC

c: Xét tứ giác ACBE có

N là trung điểm chung của AB và CE

Do đó: ACBE là hình bình hành

=>BE//AC và BE=AC

ACDB là hình bình hành

=>AC//BD và AC=BD

AC//BD

AC//BE

BD cắt BE tại B

Do đó: D,B,E thẳng hàng

mà BD=BE(=AC)

nên B là trung điểm của DE

Đúng(0)

MN

Mai Như Ý

4 tháng 12 2023 - olm

Cho tam giác ABC, vẽ điểm M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD.c)Kẻ AH vuông góc với BC, DK vuông góc BC (H,K thuộc BC). Chứng minh BK=CH d)Gọi I là trung điểm của AC, vẽ điểm E sao cho I là trung điểm của BE. Chứng minh C là trung điểm của DE

#toán 7

1

KV

Kiều Vũ Linh

4 tháng 12 2023

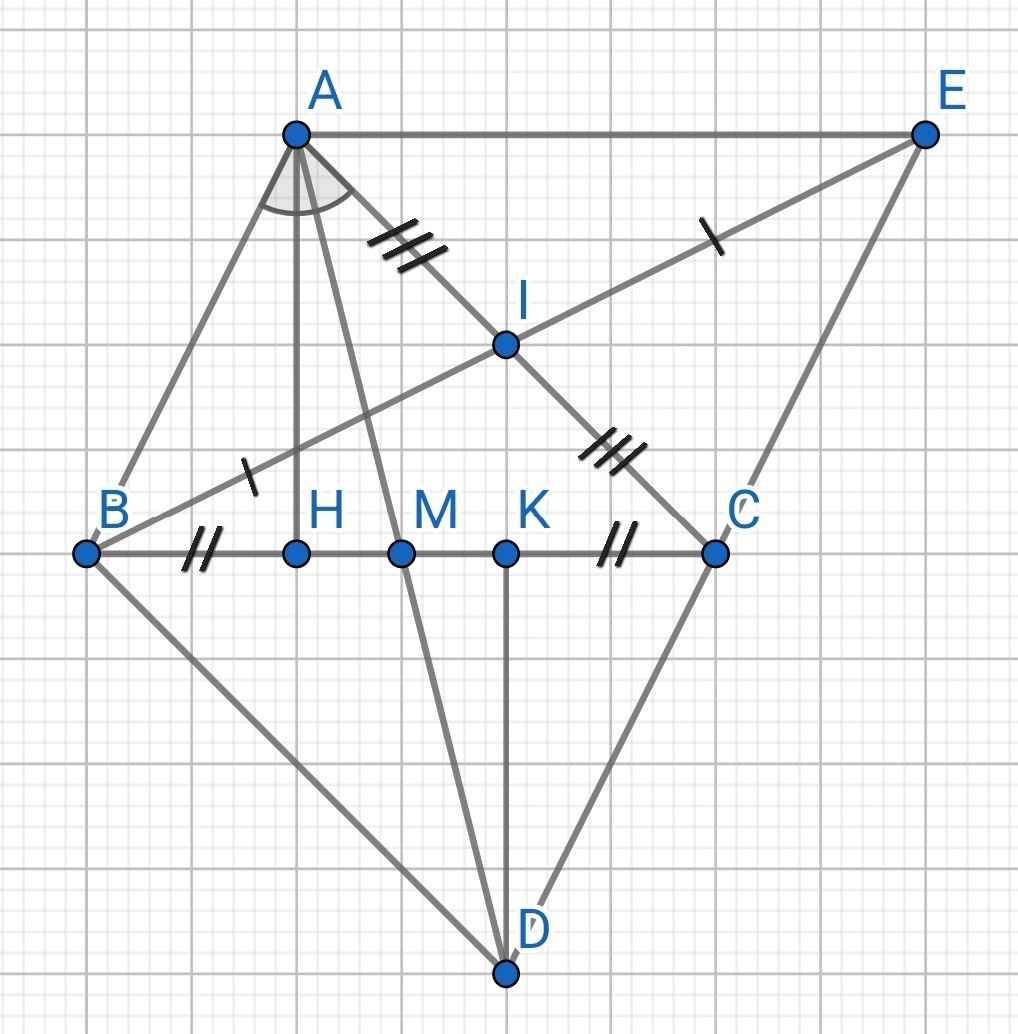loading... c) Do M là trung điểm của BC (gt)

⇒ BM = MC

Xét hai tam giác vuông: ∆AHM và ∆DKM có:

MA = MD (gt)

∠AMH = ∠DMK (đối đỉnh)

⇒ ∆AHM = ∆DKM (cạnh huyền - góc nhọn)

⇒ HM = KM (hai cạnh tương ứng)

Ta có:

BK = BM + KM

CH = CM + HM

Mà BM = CM (cmt)

KM = HM (cmt)

⇒ BK = CH

d) Tứ giác ABDC có:

M là trung điểm của BC (gt)

M là trung điểm của AD (gt)

⇒ ABDC là hình bình hành

⇒ AB // DC và AB = DC

Tứ giác ABCE có:

I là trung điểm của AC (gt)

I là trung điểm của BE (gt)

⇒ ABCE là hình bình hành

⇒ AB // CE và AB = CE

Do AB // CE (cmt)

AB // DC (cmt)

⇒ C, D, E thẳng hàng (theo tiên đề Ơ-clít)

Ta có:

AB = CE (cmt)

AB = DC (cmt)

⇒ CD = CE

⇒ C là trung điểm của DE

Đúng(4)

PT

Pham Trong Bach

6 tháng 1 2019

Cho nửa đường tròn đường kính AB. Gọi M là điểm chính giữa của cung AB. Trên cung AM lấy điểm N. Trên tia đổi của tia MA lây điểm D sao cho MD = MB, trên tia đối của tia NB lấy điểm E sao cho NA = NE, trên tia đối của tia MB lấy điểm c sao cho MC = MA. Chứng minh 5 điểm A, B, C, D, E cùng thuộc một đường tròn

#Toán lớp 9

1

CM

Cao Minh Tâm

6 tháng 1 2019

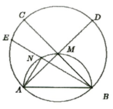
Các tam giác ∆ANE, ∆AMC và ∆BMD vuông cân

=> A E B ^ = A D B ^ = A C B ^ = 45 0

Mà AB cố định nên các điểm A, B, C, D, E cùng thuộc một đường tròn

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP