Cho nửa đường tròn tâm Y đường kính AB bán kính r .Từ A và B vẽ các tiếp tuyến AZ,BY trong cùng một nửa mặt phẳng có B là AB với nửa đường tròn tâm Y .Trên nửa đường tròn lấy điểm C ,tiếp tuyến với tâm Y tại C cắt AZ,BY lần lượt tại K và M .Chứng minh a)Ak+BM=KM b)Ak×BM=ABbình chia 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
MA,MH là tiếp tuyến
nên MA=MH
mà OA=OH
nên OM là phân giác của góc AOH(1) và HM=MA
Xét (O) có
NH,NB là tiếp tuyến
nên NH=NB và ON là phân giác của góc HOB(2)
Từ (1), (2) suy ra góc MON=1/2*180=90 độ
AM*BN=HM*HN=OH^2=R^2
b: AM+BN=HN+HM>=2*OH=AB
Dấu = xảy ra khi MN=AB
=>H trùng với O

a: Xét (O) có
CA,CM là tiếp tuyến
nênCA=CM và OC là phân giác của góc AOM(1)
mà OA=OM
nên OC là trung trực của AM
=>OC vuông góc với AM
Xét (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Xét (O)có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>MB vuông góc MA
=>MB//OC
b: Từ (1), (2) suy ra góc COD=1/2*180=90 độ
=>OC vuông góc với OD
mà OM vuông góc DC
nên MC*MD=OM^2
=>AC*BD=R^2
c: Gọi H là trung điểm của CD
Xét hình thang ABDC có
H,O lần lượtlà trung điểm của CD,AB
nên HO là đường trung bình
=>HO//AC//BD
=>HO vuông góc với AB
=>AB là tiếp tuyến của (H)

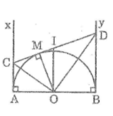
Theo tính chất tiếp tuyến, ta có:
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Suy ra tứ giác ABDC là hình thang
Gọi I là trung điểm của CD
Khi đó OI là đường trung bình của hình thang ABDC
Suy ra: OI // AC ⇒ OI ⊥ AB
Suy ra: IC = ID = IO = (1/2).CD (tính chất tam giác vuông)
Suy ra I là tâm đường tròn đường kính CD. Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.

a: Xét tứ giác OBDM có
góc OBD+góc OMD=180 độ
=>OBDM là tư giác nội tiếp
c: Xét ΔKOB và ΔKFE có
góc KOB=góc KFE
góc OKB=góc FKE
=>ΔKOB đồng dạng với ΔKFE
=>KO/KF=KB/KE
=>KO*KE=KB*KF

a: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA
Xét (O) có
DB là tiếp tuyến
DM là tiếp tuyến
Do đó: DB=DM
Ta có: MC+MD=DC
nên DC=CA+DB

