a) 4x+13/5x(x-7) + x-48/5x(7-x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
30 tháng 11 2018
a, \(\dfrac{4x+13}{5x\left(x-7\right)}-\dfrac{x-48}{5x\left(7-x\right)}\)
\(=\dfrac{4x+13}{5x\left(x-7\right)}+\dfrac{x-48}{5x\left(x-7\right)}\)
\(=\dfrac{4x+13+x-48}{5x\left(x-7\right)}\)
\(=\dfrac{5x-35}{5x\left(x-7\right)}\)
\(=\dfrac{5\left(x-7\right)}{5x\left(x-7\right)}=\dfrac{1}{x}\)
b, \(\dfrac{1}{x-5x^2}-\dfrac{25x-15}{25x^2-1}\)
\(=\dfrac{1}{x\left(1-5x\right)}+\dfrac{25x-15}{\left(1-5x\right)\left(1+5x\right)}\)
\(=\dfrac{1+5x}{x\left(x-5x\right)\left(1+5x\right)}+\dfrac{x\left(25x-15\right)}{x\left(1-5x\right)\left(1+5x\right)}\)
\(=\dfrac{1+5x+25x^2-15x}{x\left(1-5x\right)\left(1+5x\right)}\)\(=\dfrac{25x^2-10x+1}{x\left(1-5x\right)\left(1+5x\right)}=\dfrac{\left(5x-1\right)^2}{x.\left(1-5x\right)\left(1+5x\right)}\)
\(=\dfrac{\left(5x-1\right)^2}{-x\left(5x-1\right)\left(1+5x\right)}\) \(=\dfrac{-\left(5x-1\right)}{x\left(1+5x\right)}\)
4 tháng 12 2016
a)\(dk,x\ne7;x\ne0\)
\(\frac{4x+13}{5x\left(x-7\right)}-\frac{x-48}{5x\left(7-x\right)}=\frac{4x+13}{5x\left(x-7\right)}+\frac{x-48}{5x\left(x-7\right)}=\frac{\left(4x+13\right)+\left(x-48\right)}{5x\left(x-7\right)}\\ \)
\(=\frac{5x-35}{5x\left(x-7\right)}=\frac{5\left(x-7\right)}{5x\left(x-7\right)}=\frac{1}{x}\)
b)
\(\frac{1}{x-5x^2}-\frac{25x-15}{25x^2-1}=\frac{1}{x\left(1-5x\right)}+\frac{25x-15}{1-\left(5x\right)^2}=\frac{1}{x\left(1-5x\right)}+\frac{25x-15}{\left(1-5x\right)\left(1+5x\right)}\)
\(\frac{1+5x}{x\left(1-5x\right)\left(1+5x\right)}+\frac{x\left(25x-15\right)}{x\left(1-5x\right)\left(1+5x\right)}=\frac{25x^2-15x+5x+1}{x\left(1-5x\right)\left(1+5x\right)}=\frac{25x^2-10x+1}{x\left(1-5x\right)\left(1+5x\right)}\)
19 tháng 2 2022
a: \(\Leftrightarrow7\left(7-3x\right)+12\left(5x+2\right)=84\left(x+13\right)\)
\(\Leftrightarrow49-21x+60x+24=84x+1092\)
\(\Leftrightarrow39x-84x=1092-73\)
=>-45x=1019
hay x=-1019/45
b: \(\Leftrightarrow21\left(x+3\right)-14=4\left(5x+9\right)-7\left(7x-9\right)\)
=>21x+63-14=20x+36-49x+63
=>21x+49=-29x+99
=>50x=50
hay x=1
c: \(\Leftrightarrow7\left(2x+1\right)-3\left(5x+2\right)=21x+63\)
=>14x+7-15x-6-21x-63=0
=>-22x-64=0
hay x=-32/11
d: \(\Leftrightarrow35\left(2x-3\right)-15\left(2x+3\right)=21\left(4x+3\right)-17\cdot105\)
=>70x-105-30x-45=84x+63-1785
=>40x-150-84x+1722=0
=>-44x+1572=0
hay x=393/11
CM
30 tháng 12 2017
a, x - 3 : 2 = 5 14 : 5 12
=> x - 3 : 2 = 5 2
=> x - 3 : 2 = 25
=> x – 3 = 25
=> x = 53
b, 30 : x - 7 = 15 19 : 15 18
=> 30 : x - 7 = 15
=> x – 7 = 2
=> x = 9
c, x 70 = x
=> x 70 - x = 0
=> x ( x 69 - 1 ) = 0
=> 
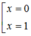
d, 2 x + 1 3 = 9 . 81
=> 2 x + 1 3 = 9 3
=> 2x + 1 = 9
=> x = 4
e, 5 x + 5 x + 2 = 650
=> 5 x 1 + 5 2 = 650
=> 5 x . 26 = 650
=> 5 x = 25
=> x = 2
f, 4 x - 1 2 = 25 . 9
=> 4 x - 1 2 = 5 2 . 3 2
=> 4 x - 1 2 = 15 2
=> 4x – 1 = 15
=> x = 4
NT
2
24 tháng 4 2017
a ) \(5x+4=2x+13\)
\(\Leftrightarrow5x-2x=13-4\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\)
Vậy tập nghiệm của phương trình là S = {3}
b ) \(\left(x+2\right)\left(x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x-7=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=7\end{matrix}\right.\)
Vậy tập nghiệm của phương trình là \(S=\left\{-2;7\right\}\)
c ) \(\left|x-2\right|=2x+14\) ( 1 )
+ ) \(\left|x-2\right|=x-2\). Khi \(x-5\ge0\Leftrightarrow x\ge5\)
\(\left(1\right)\Leftrightarrow x-2=2x+14\)
\(\Leftrightarrow x-2x=14+2\)
\(\Leftrightarrow-x=16\Leftrightarrow x=-16\) ( Loại )
+ ) \(\left|x-5\right|=-x+5.\) Khi \(x-5< 0\Leftrightarrow x< 5\)
\(\left(1\right)\Leftrightarrow-x+2=2x+14\)
\(\Leftrightarrow-3x=12\)
\(\Leftrightarrow x=-4\) ( Thõa mãn )
Vậy ................
d ) \(4x-7< 17-2x\)
\(\Leftrightarrow4x+2x< 17+7\)
\(\Leftrightarrow6x< 24\)
\(\Leftrightarrow x< 4\)
Vậy ........
24 tháng 4 2017
a) 5x + 4 = 2x +13
<=> 5x - 2x = 13- 4
<=> 3x = 9
<=> x = 3
Vậy phương trình có tập nghiệm S = { 3 }
b) (x+2). (x-7) = 0
=> \(\left[{}\begin{matrix}x+2=0\\x-7=0\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}x=-2\\x=7\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S= { -2;7}
c)
khi x \(\ge\) 2 thì\(\left|x-2\right|\) = x - 2 khi đó phương trình có dạng :
x - 2 = 2x + 14
<=> x - 2x = 14+2
<=> -x = 16
<=> -x. (-1)= 16. (-1)
<=> x = -16 (loại )
khi x < 2 thì \(\left|x-2\right|\) = -x + 2 khi đó phương trình có dạng :
-x + 2 = 2x + 14
<=> -x - 2x = 14-2
<=> -3x = 12
<=> x = -4 (nhận)
Vậy phương trình có tập nghiệm S= { -4 }
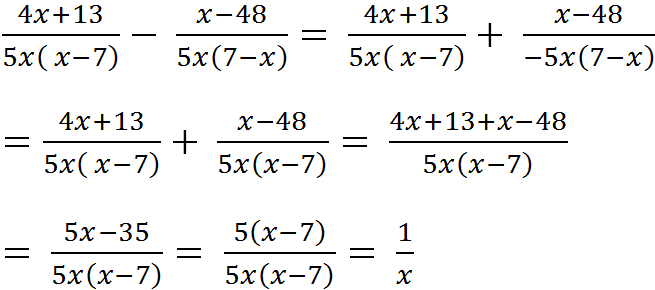
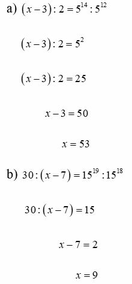
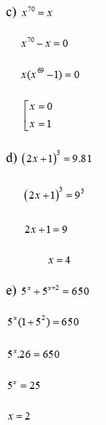
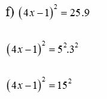
\(=\dfrac{4x+13-x+48}{5x\left(x-7\right)}=\dfrac{3x+61}{5x\left(x-7\right)}\)