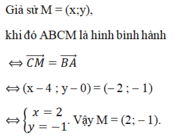Trên mặt phẳng tọa độ Oxy cho các điểm A(1;2), B(3;4). Điểm M(x;y) nằm trên trục hoành sao cho MA+MB có giá trị nhỏ nhất, khi đó 3x+y=.....
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Ta có khoảng cách từ A đến trục Ox bằng 6 > R.
Đường tròn (A; R) cắt trục Ox tại 2 điểm phân biệt .
Khoảng cách từ A đến trục Oy bằng 5 = R..
Do đó, đường tròn (A; R) tiếp xúc với trục Oy.

\(a,\) Thay \(x=3;y=4\Rightarrow\dfrac{4}{3}\cdot3=4\) (đúng)
Vậy \(A\left(3;4\right)\in y=\dfrac{4}{3}x\)

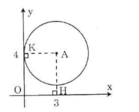
Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.

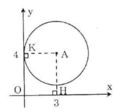
Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.

Do A(2; 4) nên A cách trục Ox 2 đơn vị, cách trục Oy 4 đơn vị
Khi đó đường tròn (A; 2) tiếp xúc với trục Ox và không giao nhau với trục Oy

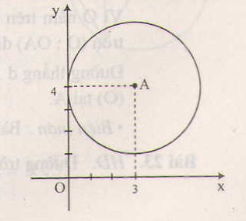
- Khoảng cách từ tâm A đến trục Ox là 4.
Vậy d>R, do đó đường tròn và trục Ox không giao nhau.
- Khoảng cách từ tâm A tới trục Oy là 3.
Vậy d=R, do đó đường tròn và trục Oy tiếp xúc nhau.

\(\text{Đặt }M\left(x;y\right)\\ \overrightarrow{MB}\left(-2-x,2-y\right);\overrightarrow{MC}\left(-x,1-y\right)\\ \left|\overrightarrow{MB}\right|=\left|2\overrightarrow{MC}\right|\Leftrightarrow\sqrt{\left(-2-x\right)^2+\left(2-y\right)^2}=2\sqrt{\left(-x\right)^2+\left(1-y\right)^2}\\ \Leftrightarrow x^2+4x+4+y^2-4y+4=2x^2+2y^2-4y+2\\ \Leftrightarrow x^2+y^2-4y-6=0\\ \text{Mà }M\in Ox\Leftrightarrow y=0\Leftrightarrow x^2-6=0\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{6}\\x=-\sqrt{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}M\left(\sqrt{6};0\right)\\M\left(-\sqrt{6};0\right)\end{matrix}\right.\)