Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C. Trên tia Oy lấy hai điểm B,D sao cho OA = OB, AC = BD.
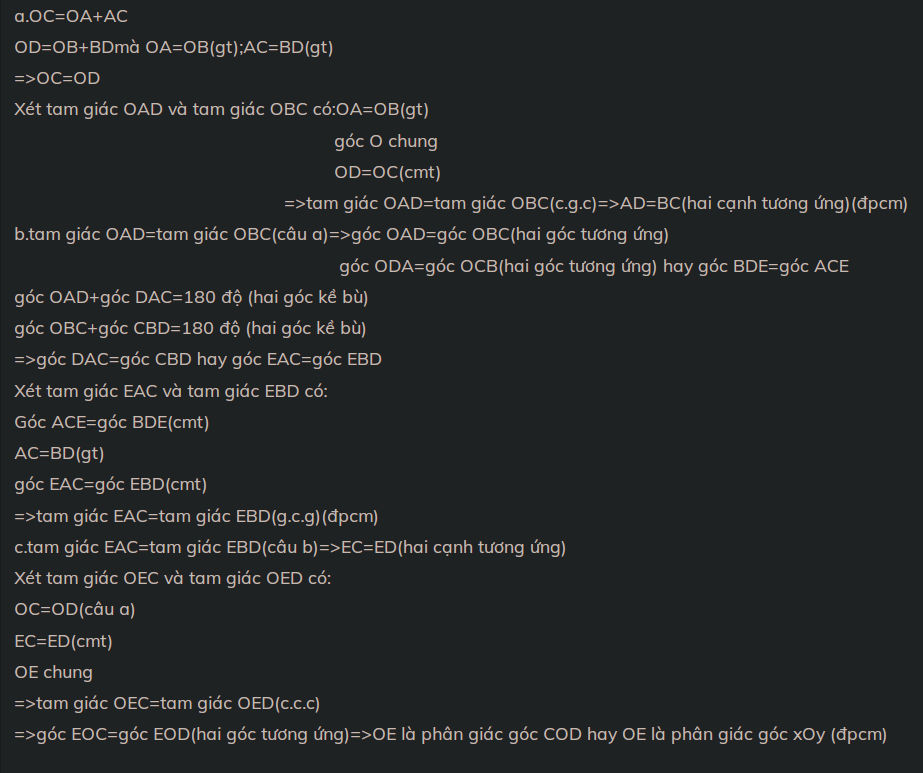
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm AD và BC. Chứng minh: EAC = EBD
c) Chứng minh: OE là phân giác của góc xOy, OE vuông góc với CD.
Các bạn giúp mik vs