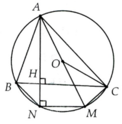
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O),đường cao AH.Kẻ đường kính AM.
a.Tính góc ACM.
b.Chứng minh góc BAH = góc OA
c.Gọi N là giao điểm của AH với đường tròn (O).Tứ giác BCMN là hình gì?Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 12 2021
\(a,\widehat{ACM}=90^0\) (góc nt chắn nửa đg tròn)
\(b,\widehat{BAH}+\widehat{ABH}=90^0;\widehat{OAC}+\widehat{AMC}=90^0\left(\widehat{ACM}=90^0\right)\)
Mà \(\widehat{ABH}=\widehat{AMC}\left(=\dfrac{1}{2}sđ\stackrel\frown{AC}\right)\)
Do đó \(\widehat{BAH}=\widehat{OAC}\)
26 tháng 1 2022
a: Xét (O) có
ΔACM nội tiếp
AM là đường kính
Do đó: ΔACM vuông tại C
hay \(\widehat{ACM}=90^0\)
b: \(\widehat{OAC}+\widehat{AMC}=90^0\)
\(\widehat{BAH}+\widehat{ABC}=90^0\)
mà \(\widehat{AMC}=\widehat{ABC}\)
nên \(\widehat{OAC}=\widehat{BAH}=\widehat{OCA}\)
R
26 tháng 1 2022
Xét \(\Delta OAC\) có : \(OA=OC\left(=R\right)\left(gt\right)\)
\(\Rightarrow\Delta OAC\) cân tại O
\(\Rightarrow\widehat{OAC}=\widehat{ACO\left(2\right)}\)
Từ (1) và (2) \(\Rightarrow\widehat{BAH=\widehat{OCA}}\)
c) Xét \(\left(O\right)\), có : \(\widehat{ANM=90^0}\)
\(\Rightarrow MN\pm AN\)
\(MàBC\pm AN\left(gt\right)\)
\(\Rightarrow MN=BC\)
Xét tam giác \(BNMC\)\(cóMN=BC\left(cmt\right)\)
Tam giác BNMC là hình thang
Mà bốn đỉnh B,M,N,C
Vậy BMNC là tam giác cân
23 tháng 1 2022
a: Xét (O) có
ΔACM nội tiếp
AM là đường kính
Do đó: ΔACM vuông tại C
b: \(\widehat{BAH}+\widehat{ABC}=90^0\)
\(\widehat{OAC}+\widehat{AMC}=90^0\)
mà \(\widehat{ABC}=\widehat{AMC}\left(=\dfrac{sđ\stackrel\frown{AC}}{2}\right)\)
nên \(\widehat{BAH}=\widehat{OAC}=\widehat{OCA}\)
CM
7 tháng 5 2019
a, Ta có A C M ^ = 90 0 (góc nội tiếp)
b, Ta có ∆ABH:∆AMC(g.g)
=> B A H ^ = O A C ^ ; O C A ^ = O A C ^
=> B A H ^ = O C A ^
c, A N M ^ = 90 0
=> MNBC là hình thang
=> BC//MN => sđ B N ⏜ = sđ C M ⏜
=> C B N ^ = B C M ^ nên BCMN là hình thang cân
NT
1 tháng 3 2016
a)Gọi I là trung điểm của tam giác BC
Áp dụng đường trung tuyến cạnh huyền của tam giác EBC và DBC
=>IE=ID=IB=IC
=> tứ giác BCDE nội tiếp. tâm đường tròn là I
b)AFK=90 ( dg cao thứ 3)
ACK=90 (chắn nữa dg tròn)
=>AFB=ACK
c)BD vg góc với AC
ACK=90 =>CK vg góc với AC
=>CK song song với BH
tuong tu CH song song voi BK
=>BHCK là hinh binh hanh
*vì I là trung điểm của BC
=>I cung la trung diem cua HK
=>H,I,K thang hang
23 tháng 1 2021
a, ABDC nội tiếp
=> ˆBAH = ˆBCD
ACED nội tiếp
=> OAC^ = CDE^
Lại có ΔDEA nội tiếp đường tròn đường kínhAE
=> DE ⊥ AD
mà AD ⊥ BC
=> DE // BC=>BCD^ =CDE^ ( so le trong)
=>BAH^ = OAC^
b, DE // BC=> BDEC là hình thang (*)
Lại có:
DBC^ = DAC^ ( BDAC nội tiếp) (1)
BCE^= EAB^ ( ABEC nội tiếp) (2)
Lại có: BAH^ = OAC^
=> BAH^ + HAO^ = OAC^ + ˆHAO
=> EAB^ = DAC^ (3)
Từ (1) (2) (3) => DBC^= BCE^ (**)
từ (*) và (**) => BCED là hình thang cân
\(a,\widehat{ACM}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(b,\widehat{ABC}=\widehat{AMC}=\dfrac{1}{2}sđ\mathop{AC}\limits^{\displaystyle\frown}\)
Mà \(\widehat{ABH}+\widehat{ABC}=\widehat{OAC}+\widehat{AMC}=90^0\)
Do đó \(\widehat{ABH}=\widehat{OAC}\)
\(c,\widehat{ANM}=90^0\) (góc nội tiếp chắn nửa đường tròn)
Do đó \(MN\bot AN\)
Mà \(BC\bot AN \Rightarrow BC//MN\)
Do đó BCMN là hình thang
Mà \(B,M,N,C\in (O)\)
Vậy BCMN là hình thang cân