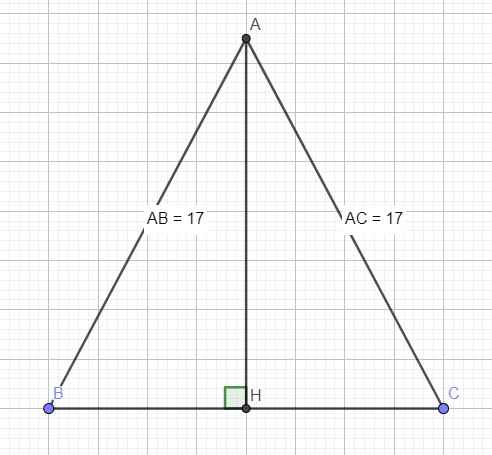
Cho tam giác ABC cân tại A. Đường cao AH bằng một nửa BC. Vậy góc BAC bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì AH bằng một nửa BC=>AH=BH=CH
=>tam giác BAH=tam giác CAH(2 cạnh góc vuông)
=>góc B=góc C
Ta có tam giác ABH cân tại H(AH=HB)
=>góc BAH= góc B(tính chất tam giác cân)
Tương tự ta có: =>góc HAC=góc C
góc B=góc C(CMT)
Mà góc B=góc BAH
góc C = góc CAH
=>góc BAC=B+C(=BAH+CAH)
Mà B=C=>BAC=2B(C) mà BAC+B+C=1800=>A=1800:4=250
Vậy BAC =250


CHÚ Ý: đây là định lý đảo của trung tuyến trong tam giác vuông
Do tam giác ABC cân tại A nên AH là đường cao đồng thời cũng là đường trung tuyến
mà theo ĐL đảo ủa đường trung tuyến thì nếu trung tuyến = một nửa cạnh huyền thì tam giác đó vuông
=> tam giác ABC vuông cân tại A
=> A=90


Do tam giác ABC cân tại A nên AH là đường cao đồng thời là trung tuyến
\(\Rightarrow\) H là trung điểm BC \(\Rightarrow BH=CH=\dfrac{1}{2}BC=8\)
Áp dụng định lý Pitago cho tam giác vuông ABH:
\(AH=\sqrt{AB^2-BH^2}=15\)
\(cosB=\dfrac{BH}{AB}=\dfrac{8}{17}\Rightarrow B\approx62^0\) \(\Rightarrow C=B=62^0\)
\(\Rightarrow A=180^0-\left(B+C\right)=56^0\)

Gọi \(IE\) là khoảng cách từ \(I\) đến cạnh \(AB\) của \(\Delta ABC\) \(\left(E\in AB\right)\)
\(\Delta ABC\) cân tại \(A\) có \(AH\) là đường cao nên cũng là đường trung tuyến, đồng thời \(AH\) vừa là đường phân giác
Do đó, \(BH=HC=\frac{1}{2}.BC\)
Ta có: \(AH,\) \(BD\) lần lượt là phân giác góc \(A,\) góc \(B\) và cùng đi qua điểm \(I\)
nên điểm \(I\) cách đều ba cạnh của \(\Delta ABC\) (theo đ/lý hai suy ra từ tính chất ba đường phân giác của tam giác)
Khi đó, \(IE=IH=IF\)
Vì \(BI\) là phân giác (theo gt) nên theo tính chất đường phân giác, ta có:
\(\frac{IH}{IA}=\frac{BH}{AB}=\frac{\frac{1}{2}.BC}{AB}=\frac{1}{2}.\frac{2}{3}=\frac{1}{3}\) (do \(\frac{BC}{AB}=\frac{2}{3}\))
Áp dụng tính chất tỉ lệ thức, ta được:
\(\frac{IH}{IA}=\frac{1}{3}\)
\(\Rightarrow\) \(\frac{IH}{IH+IA}=\frac{1}{1+3}\)
\(\Leftrightarrow\) \(\frac{IH}{AH}=\frac{1}{4}\)
nên \(IH=\frac{1}{4}.AH=\frac{1}{4}.26,1=6,525\)
Do đó, \(IE=IF=6,525\)
Vậy, khoảng cách từ \(I\) đến mỗi cạnh của tam giác là \(6,525\)
AH bằng một nửa BC=>AH=BH=CH=>tam giác BAH=tam giác CAH(2 cạnh góc vuông)=>góc B=góc C
ta có tam giác ABH cân tại H(AH=HB)=>góc BAH= góc B(tính chất tam giác cân)
tương tự=>góc HAC=góc C
góc B=góc C(CMT)
mà góc B=gócBAH
góc C=góc CAH
=>góc BAC=B+C(=BAH+CAH)
mà B=C=>BAC=2B(C) màBAC+B+C=180 độ=>A=180 độ:4=25 độ