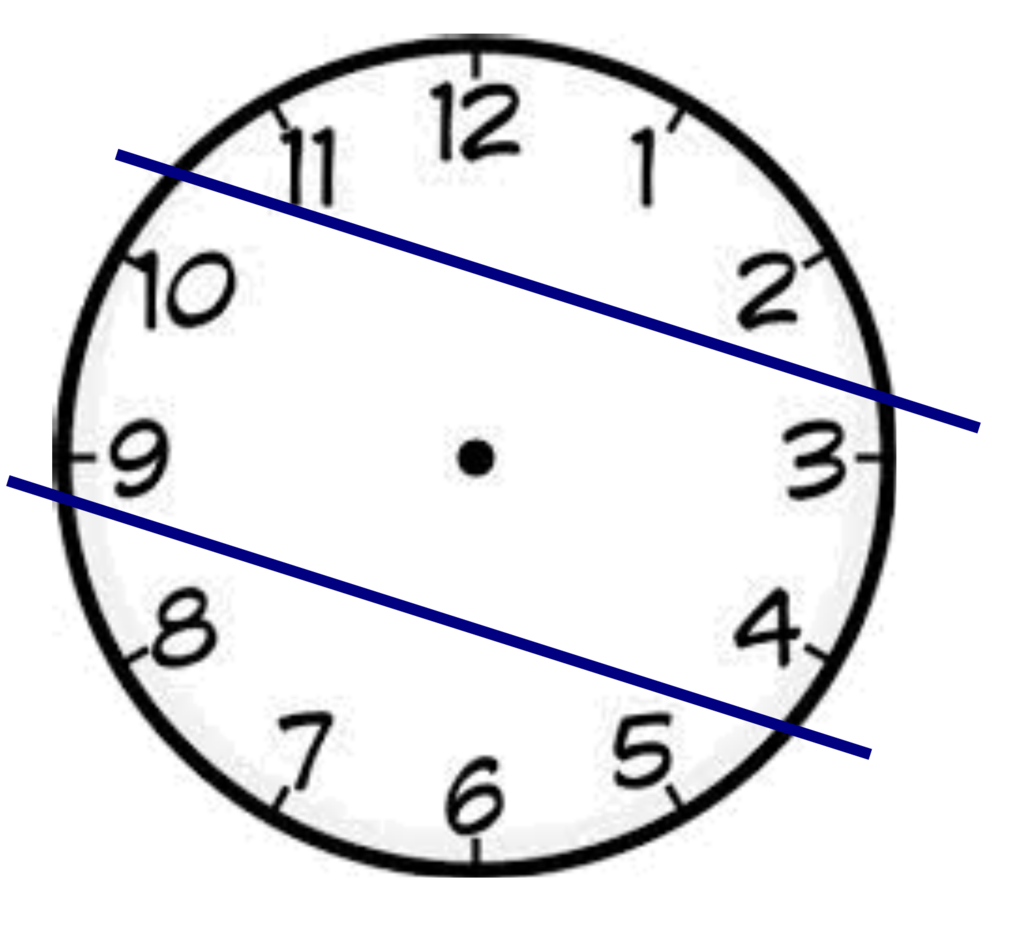
HÃY VẼ 2 ĐOẠN THẲNG AB VÀ CD SAO CHO 2 ĐOẠN THẲNG ĐÓ CHIA MẶT ĐỒNG HỒ THÀNH 3 PHẦN MÀ TỔNG CÁC SỐ TRONG 3 PHẦN ĐÓ BẰNG NHAU.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VT
Vũ Thu Hiền
15 tháng 3 2021
Hình tròn tâm O có bán kính là 4cm.Đường kính của hình tròn đó là!
Đúng(0)
Những câu hỏi liên quan
NK
0
W
18 tháng 7 2017
Tổng các số trên mặt đồng hồ là: 1 + 2 + ... + 12 = (1 + 12) + (2 + 11) + ... + (6 + 7) = 13 + 13 + ... + 13 = 6x13 = 78.
Nếu chia 3 phần có tổng bằng nhau thì mỗi phần có tổng là: 78:3 = 26. Bằng cách ghép các số liền nhau để được tổng là 26, sẽ có 2 phần gồm các số đứng cạnh nhau mà tổng bằng 26 là: (11, 12, 1, 2) và (5, 6, 7, 8). Hai phần này cắt ra thì phần còn lại gồm các số (9, 10, 3, 4) cũng có tổng là 26. Vậy đáp án là: Phần 1 là (1, 2, 12, 11); Phần 2 là (3, 4, 9, 10); Phần 3 là (5, 6, 7, 8) xem hình vẽ:
2 tháng 10 2018
Tổng các số ở phần trên là :
10 + 11 + 12 + 1 + 2 + 3 = 39
Tổng các số ở phần dưới là :
4 + 5 + 6 + 7 + 8 + 9 = 39
Tổng của cả 2 phần đều bằng nhau
DV
Hãy kẻ hai đường thẳng để chia mặt đồng hồ sao cho tổng các số trong mỗi
phần được chia đều bằng nhau
2
CM
27 tháng 9 2017
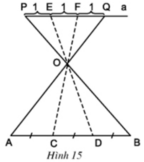
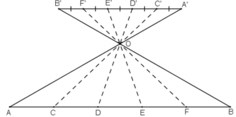
a) - Mô tả cách làm:
+ Vẽ đoạn thẳng PQ song song với AB, PQ có độ dài bằng 3 đơn vị.
+ E, F nằm trên PQ sao cho PE = EF = FQ = 1. Xác định giao điểm O của hai đoạn thẳng PB và QA
+ Vẽ các đường thẳng EO, FO cắt AB tại C và D.
Khi đó ta được AC = CD = DB.
- Chứng minh AC = CD = DB:
Theo hệ quả định lý Ta-let ta có:
ΔOAC có FQ // AC (F ∈ OC, Q ∈ OA) ⇒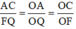 
ΔOCD có EF // CD (E ∈ OD, F ∈ OC) ⇒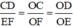 
ΔODB có PE // BD (P ∈ OB, E ∈ OD) ⇒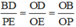 
Từ 3 đẳng thức trên suy ra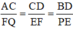 
Mà FQ = EF = PE ⇒ AC = CD = DB (đpcm).
b) Tương tự chia đoạn thẳng AB thành 5 đoạn bằng nhau thực hiện như hình vẽ sau
Ngoài cách trên, ta có thể chia một đoạn thẳng thành 5 đoạn bằng nhau bằng cách vẽ thêm một đoạn thẳng AC bằng 5 đơn vị, chia đoạn thẳng AC thành 5 đoạn thẳng bằng nhau, mỗi đoạn bằng 1 đơn vị: AD = DE = EF = FG = GC.
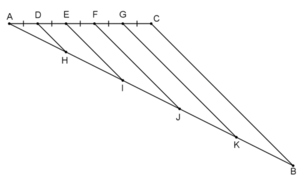
Từ các điểm D, E, F, G ta kẻ các đường thẳng song song với BC, cắt AB tại H, I, J, K. Khi đó ta thu được các đoạn thẳng AH = HI = IJ = JK = KB.
CM
23 tháng 6 2017
Ta tính được tổng các số trên mặt đồng hồ là 78.
Vậy chia thành 3 phần bằng nhau thì tổng các số ở một phần là 26.
