Một lò xo có chiều dài tự nhiên 35cm và có độ cứng 200 N/m. Giữ cố định một đầu vào một đầu treo vật .Tìm khối lượng vật treo biết chiều dài lò xo sau khi treo vật là 38cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
Hà Đức Thọ
Admin
6 tháng 11 2015
a) Độ biến dạng của lò xo khi vật ở VTCB: \(\Delta l_0=18-14=4cm=0,04m\)
Ở vị trí cân bằng lực đàn hồi cân bằng với trọng lực của vật: \(P=F_{dh}\Rightarrow mg=k\Delta l_0\Rightarrow k=\frac{mg}{\Delta l_0}=\frac{0,2.10}{0,04}=50\)(N/m)
b) Treo thêm m' ta có: \(\Delta l_0'=19-14=5cm=0,05m\)
\(m+m'=\frac{k.\Delta l_0'}{g}=\frac{50.0,05}{10}=0,25kg=250g\)
\(\Rightarrow m'=250-200=50g\)
VT
20 tháng 9 2017
Ta có:
k - không đổi
Khi cân bằng, ta có lực đàn hồi cân bằng với trọng lực, ta có:
+ Khi treo vật 600g
m 1 g = k . ( l 1 − l 0 ) ↔ 0 , 6.10 = k . ( 0 , 23 − l 0 ) (1)
+ Khi treo vật 800g
m 2 g = k . ( l 2 − l 0 ) ↔ 0 , 8.10 = k . ( 0 , 24 − l 0 ) (2)
Giải hệ (1) và (2), ta được:
l 0 = 0 , 2 m k = 200 N / m
Đáp án: A
H9
HT.Phong (9A5)
CTVHS
2 tháng 5 2023
a) Độ biến dạng của lò xo là:
\(\Delta l=l-l_0=22-20=2\left(cm\right)=0,02cm\)
Ta có: \(P+F=0\) (ở vị trí cân bằng)
\(\Rightarrow P=F\)
Mà \(P=mg\) và \(F=k\Delta l\)
\(\Rightarrow mg=k\Delta l\)
\(\Leftrightarrow k=\dfrac{mg}{\Delta l}\)
\(\Leftrightarrow k=\dfrac{0,5.10}{0,02}\)
\(\Leftrightarrow k=250N/m\)
b) Độ dài lò xo dãn ra:
Ta có: \(P=F\)
\(\Leftrightarrow\left(m_1+m_2\right).g=k.\Delta l\)
\(\Leftrightarrow\Delta l=\dfrac{\left(m_1+m_2\right).g}{k}\)
\(\Leftrightarrow\Delta l=\dfrac{\left(0,5+0,3\right).10}{250}=0,032\left(m\right)=3,2\left(cm\right)\)
Chiều dài của lò xo:
\(l=\Delta l+l_0=3,2+20=23,2\left(cm\right)\)
VT
13 tháng 6 2017
Lò xo cân bằng: F = P ⇔ k Δ l = m g
Khi treo vật m1: k ( l − l 0 ) = m 1 g 1
Khi treo thêm m2 : k ( l 2 − l 0 ) = ( m 1 + m 2 ) g 2
Từ (1) và (2) ⇒ l 0 = 20 c m ⇒ k = 97 N / m
VT
28 tháng 2 2017
Chọn đáp án C
Lò xo cân bằng: F=P
Khi treo vật m1:
(1)
Khi treo thêm m2 :
(2)
Từ (1) và (2) 
VT
15 tháng 8 2017
Chọn đáp án B
Ta có:
∆ℓ1 = 44 – 27 = 17 cm = 0,17 m.
P1 = k∆ℓ1
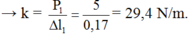
Có:
∆ℓ2 = 35 – 27 = 8cm = 0,08m
P2 = k.∆ℓ2 = 29,4.0,08 = 2,35N
Ta có :
\(k.\Delta l=mg\Leftrightarrow m=\dfrac{k\Delta l}{g}=\dfrac{200.\left(0,38-0,35\right)}{10}=0,6\left(kg\right)\)