Giúp mik câu 33 34 đi ạ 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Y
21 tháng 12 2023
Câu 34:
\(u_0=acos\left(\omega t+\dfrac{\pi}{2}\right)\left(cm\right)\)
Tại \(t=\dfrac{\pi}{\omega}\Rightarrow u_M=acos\left(\omega.\dfrac{\pi}{\omega}+\dfrac{\pi}{2}-\dfrac{\pi}{2}\right)\Leftrightarrow-2=acos\left(\pi\right)\)
\(\Leftrightarrow-2=a\left(-1\right)\Leftrightarrow a=2\left(cm\right)\)
\(\Rightarrow\) Chọn C
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
31.
\(y'=4x^3+1\)
Tiếp tuyến vuông góc với \(d\) nên có hệ số góc \(k=5\)
Gọi hoành độ tiếp điểm là \(x_0\Rightarrow4x_0^3+1=5\Rightarrow x_0^3=1\)
\(\Rightarrow x_0=1\Rightarrow y_0=2\)
Phương trình: \(y=5\left(x-1\right)+2\Leftrightarrow y=5x-3\)
33.
Vận tốc của chất điểm: \(v\left(t\right)=S'\left(t\right)=5-6t\)
\(v\left(t\right)=3\Rightarrow5-6t=3\Rightarrow t=\dfrac{1}{3}\)
\(\Rightarrow S=5.\dfrac{1}{3}-3.\left(\dfrac{1}{3}\right)^2=1,33\left(m\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 4 2022
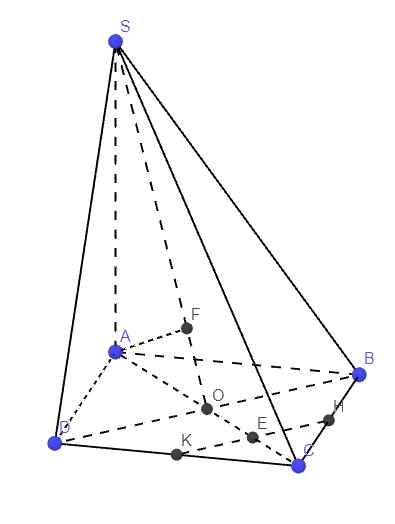
Gọi E là giao điểm HK và AC
\(\Rightarrow E\) là trung điểm OC \(\Rightarrow OE=\dfrac{1}{2}OC=\dfrac{1}{2}OA\)
\(\Rightarrow d\left(E;\left(SBD\right)\right)=\dfrac{1}{2}d\left(A;\left(SBD\right)\right)\)
HK là đường trung bình tam giác BCD \(\Rightarrow HK||BD\)
\(\Rightarrow d\left(HK;SD\right)=d\left(HK;\left(SBD\right)\right)=d\left(E;\left(SBD\right)\right)=\dfrac{1}{2}d\left(A;\left(SBD\right)\right)\)
Từ A kẻ \(AF\perp SO\Rightarrow AF\perp\left(SBD\right)\Rightarrow AF=d\left(A;\left(SBD\right)\right)\)
\(AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng:
\(AF=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{2a}{3}\)
\(\Rightarrow d\left(HK;SD\right)=\dfrac{1}{2}AF=\dfrac{a}{3}\)
AH
Akai Haruma
Giáo viên
20 tháng 3 2022
Câu 33:
Đặt $b=aq$ và $c=aq^2$ với $q$ là công bội
Theo bài ra ta cũng có:
$b=a+3d$ và $c=a+7d$ với $d$ là công sai
$\Rightarrow aq=a+3d$ và $aq^2=a+7d$
$\Leftrightarrow a(q-1)=3d$ và $a(q^2-1)=7d$
$\Rightarrow \frac{a(q^2-1)}{a(q-1)}=\frac{7}{3}$
$\Leftrightarrow q+1=\frac{7}{3}$
$\Leftrightarrow q=\frac{4}{3}$
Thay vào điều kiện: $a+aq+aq^2=\frac{148}{9}$ suy ra $a=4$
Vậy $q=\frac{4}{3}; a=4$. Thay vô $T$:
$T=a-b+c-d=a-aq+aq^2-aq^3$
$=a(1-q+q^2-q^3)=\frac{-100}{27}$
Đáp án C>
AH
Akai Haruma
Giáo viên
20 tháng 3 2022
Câu 34:
Trước tiên để có 3 nghiệm pb thì $m\neq 1; m\neq 3$
PT có 3 nghiệm: $1,3,m$
$3$ nghiệm này lập thành cấp số nhân theo thứ tự là:
TH1: $1,3,m$
$\Rightarrow q=3:1=3$. $m=3q=3.3=9$
TH2: $1,m,3$
$m=1.q=q>0$ do đây là csn tăng
$3=mq=q^2\Rightarrow q=\sqrt{3}$
$\Rightarrow m=\sqrt{3}$
TH3:
$m, 1,3$
$1=mq; 3=1.q$
$\Rightarrow q=3\Rightarrow m=\frac{1}{3}$
Vậy có 3 giá trị $m$ thỏa mãn. Đáp án B.
DA
17 tháng 6 2015
mình gợi ý nhé 1
1. là so sánh với 1
2 . so sánh với 0
3 . rút gọn đi rồi quy đồng lên sau đó so sánh
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
33. B là khẳng định sai
Câu này xác định rất đơn giản, AB và AC cùng thuộc mp (ABC), trong khi MN không song song và cũng ko thuộc (ABC) nên 3 vecto này ko thể đồng phẳng
34.
\(\overrightarrow{MN}=\overrightarrow{MD'}+\overrightarrow{D'C'}+\overrightarrow{C'N}=\dfrac{1}{3}\overrightarrow{AD'}+\overrightarrow{D'C'}+\dfrac{1}{3}\overrightarrow{C'D}\)
\(=\dfrac{1}{3}\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AA'}+\overrightarrow{D'C'}+\dfrac{1}{3}\overrightarrow{C'C}+\dfrac{1}{3}\overrightarrow{C'D'}\)
\(=\dfrac{1}{3}\overrightarrow{AD}+\dfrac{2}{3}\overrightarrow{D'C'}=-\dfrac{1}{3}\overrightarrow{AD}+\dfrac{2}{3}\left(B'C'+\overrightarrow{A'B'}\right)\)
\(=-\dfrac{1}{3}\overrightarrow{AD}+\dfrac{2}{3}\overrightarrow{A'C'}\)
A là đáp án đúng
33B
Cách giải đi bn còn câu 34 nữa