Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
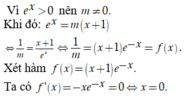
Dựa vào BBT, ta thấy phương trình có nghiệm duy nhất
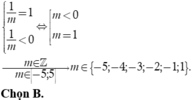
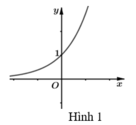
Ta có y = e x là hàm đồng biến trên ℝ và y = e x > 0 với mọi x ∈ ℝ có đồ thị (C)(xem hình 1).
Do đó:
= Nếu m < 0 thì y = m(x+1) là hàm số nghịch biến trên ℝ , có đồ thị là một đường thẳng luôn qua điểm (-1;0) nên luôn cắt đồ thị (C): y = e x tại duy nhất một điểm.
= Nếu m = 0 phương trình vô nghiệm (do y = e x > 0).
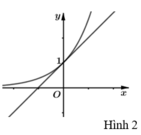
= Nếu m > 0 để phương trình có duy nhất một nghiệm khi và chỉ khi đường thẳng
là tiếp tuyến của (C) (như hình 2)
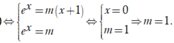
\(\sqrt{2x^2-8x+m}=x-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2-8x+m=\left(x-1\right)^2\\x-1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-6x+m-1=0\\x\ge1\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(x^2-6x+m-1=0\left(1\right)\) có nghiệm duy nhất thỏa mãn \(x\ge1\)
\(\left(1\right)\Leftrightarrow m=f\left(x\right)=-x^2+6x+1\)
Đồ thi hàm số \(y=f\left(x\right)=-x^2+6x+1\):
Dựa vào đồ thị ta được \(m=10\)
P/s: Cái này t lười vẽ bảng biến thiên nên vẽ đồ thị đó, chứ bình thường viết trong vở thì dùng bảng biến thiên nhanh hơn nhiều.
Phương trình viết lại m + 1 x = 3 m 2 - 1 x = 1 - m
Phương trình đã cho có nghiệm duy nhất khi 3 m 2 - m - 2 ≠ 0 ⇔ m ≠ 1 m ≠ − 2 3
Do m ∈ Z và m ∈ [−5; 10] ⇒ m ∈ {−5; −4; −3; −2; −1; 0; 2; 3; 4; 5; 6; 7; 8; 9; 10}.
Do đó, tổng các phần tử trong S bằng 39.
Đáp án cần chọn là: B
a: Khi m=-1 thì hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}-x+y-3=3\\x-y-2\cdot\left(-1\right)+1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-x+y=6\\x-y=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}0x=3\left(vôlý\right)\\x-y=-3\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)
b: \(\left\{{}\begin{matrix}mx+y-3=3\\x+my-2m+1=0\end{matrix}\right.\)(1)
=>\(\left\{{}\begin{matrix}mx+y=6\\x+my=2m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=6-mx\\x+m\left(6-mx\right)=2m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+6m-m^2x=2m-1\\y=6-mx\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(1-m^2\right)=-4m-1\\y=6-mx\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(m^2-1\right)=4m+1\\y=6-mx\end{matrix}\right.\)
TH1: m=1
Hệ phương trình (1) sẽ trở thành:
\(\left\{{}\begin{matrix}x\cdot0=4\cdot1+1=5\\y=6-mx\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)
=>Loại
TH2: m=-1
Hệ phương trình (1) sẽ trở thành:
\(\left\{{}\begin{matrix}x\cdot0=-4+1=-3\\y=6-mx\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)
=>Loại
Th3: \(m\notin\left\{1;-1\right\}\)
Hệ phương trình (1) sẽ tương đương với \(\left\{{}\begin{matrix}x=\dfrac{4m+1}{m^2-1}\\y=6-mx=\dfrac{6\left(m^2-1\right)-m\left(4m+1\right)}{m^2-1}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{4m+1}{m^2-1}\\y=\dfrac{6m^2-6-4m^2-m}{m^2-1}=\dfrac{2m^2-m-6}{m^2-1}\end{matrix}\right.\)
Để hệ có nghiệm duy nhất thì m/1<>1/m
=>\(m^2\ne1\)
=>\(m\notin\left\{1;-1\right\}\)
Để x nguyên thì \(4m+1⋮m^2-1\)
=>\(\left(4m+1\right)\left(4m-1\right)⋮m^2-1\)
=>\(16m^2-1⋮m^2-1\)
=>\(16m^2-16+15⋮m^2-1\)
=>\(m^2-1\inƯ\left(15\right)\)
=>\(m^2-1\in\left\{1;-1;3;-3;5;-5;15;-15\right\}\)
=>\(m^2\in\left\{2;0;4;6;16\right\}\)
=>\(m\in\left\{\sqrt{2};-\sqrt{2};0;2;-2;\sqrt{6};-\sqrt{6};4;-4\right\}\)
mà m nguyên
nên \(m\in\left\{0;2;4;-2;-4\right\}\left(2\right)\)
Để y nguyên thì \(2m^2-m-6⋮m^2-1\)
=>\(2m^2-2-m-4⋮m^2-1\)
=>\(m+4⋮m^2-1\)
=>\(\left(m+4\right)\left(m-4\right)⋮m^2-1\)
=>\(m^2-16⋮m^2-1\)
=>\(m^2-1-15⋮m^2-1\)
=>\(m^2-1\inƯ\left(-15\right)\)
=>\(m^2-1\in\left\{1;-1;3;-3;5;-5;15;-15\right\}\)
=>\(m^2\in\left\{2;0;4;6;16\right\}\)
=>\(m\in\left\{\sqrt{2};-\sqrt{2};0;2;-2;\sqrt{6};-\sqrt{6};4;-4\right\}\)
mà m nguyên
nên \(m\in\left\{0;2;4;-2;-4\right\}\left(3\right)\)
Từ (2),(3) suy ra \(m\in\left\{0;2;4;-2;-4\right\}\)
Thử lại, ta sẽ thấy m=4;m=-2 không thỏa mãn x nguyên; m=4;m=-2 không thỏa mãn y nguyên
=>\(m\in\left\{0;2;-4\right\}\)
