Cho tam giác ABC vuông tại A đường cao AH.Vẽ đường tròn (A;AH).Từ B,C kẻ các tiếp tuyển BD,CE với đường tròn (A),trong đó D,E là tiếp điểm.Chứng minh:
1)A,D,E thẳng hàng
2)BD.CE nhỏ hơn bằng \(\dfrac{BC^2}{4}\)
3)Gọi M là trung điểm CH.Đường tròn (M),đường kính CH cắt đường tròn (A) tại N (N khác H).Chứng minh:CN//AM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta co tam giac AHB vuong tai H(gt)=>goc ABH + goc BAH=90 độ(1)
tam giac BAC vuong tại A (gt)=>goc BAH +goc CAH=90độ(2)
tu 1 va 2=>goc ABH=gocCAH(3)
tam giac AON co ON=OA(cung ban kinh)=>tam giac AON can=>goc OAN= goc ONA
hay goc CAH = goc ONA(4)
TU 3 VA 4=>goc ONA=goc ABH hay goc ANH=MBC
ma goc ANM+CNM=900=>goc MBC+goc MNC=1800=>DPCM

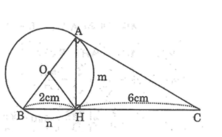
Trong tam giác ABC vuông tại A nên ta có:
A B 2 = BH.BC =2.(2+6)=2.8=16
suy ra AB = 4cm
Diện tích hình tròn tâm (O) là :
S=π. A B / 2 2 = π. 4 / 2 2 = 4π ( c m 2 )

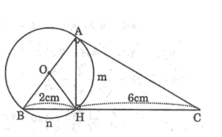
Ta có AB=4cm ⇒ OB =2cm
Tam giác OBH có OB = OH =HB = 2cm nên tam giác OBH đều
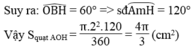

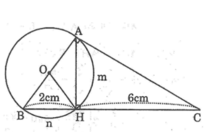
Trong tam giác vuông ABC có:
A H 2 = HB.HC =2.6=12
Suy ra: AH =2. 3 cm
Diện tích tam giác AHB:
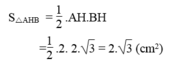
Tổng diện tích hai hình viên phân AmH và BnH bằng diện tích nửa hình tròn tâm O đường kính AB trừ diện tích tam giác AHB có:
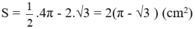

a: ΔBAD cân tại B
mà BH là đường cao
nên BH là phân giác của góc ABD
XétΔCAB và ΔCDB có
BA=BD
\(\widehat{ABC}=\widehat{DBC}\)
BC chung
Do đó: ΔCAB=ΔCDB
=>\(\widehat{CAB}=\widehat{CDB}=90^0\)
=>CD là tiếp tuyến của (B;BA)
b: I đối xứng B qua AH
=>AH là đường trung trực của BI
=>AH\(\perp\)BI tại trung điểm của BI
mà AH\(\perp\)BC
và BC,BI có điểm chung là B
nên B,I,C thẳng hàng
AH\(\perp\)BI tại trung điểm của BI
=>AH\(\perp\)BC tại trung điểm của BI
mà AH\(\perp\)BC tại H
nên H là trung điểm của BI
ΔBAD cân tại B
mà BH là đường cao
nên H là trung điểm của AD
Xét tứ giác ABDI có
H là trung điểm chung của AD và BI
nên ABDI là hình bình hành
Hình bình hành ABDI có BA=BD
nên ABDI là hình thoi
=>ID//AB
mà AB\(\perp\)AC
nên ID\(\perp\)AC
Xét ΔCAD có
CH,DI là đường cao
CH cắt DI tại I
Do đó: I là trực tâm của ΔCAD
=>AI\(\perp\)CD tại E
Gọi K là trung điểm của AC
=>K là tâm của đường tròn đường kính AC
Xét tứ giác AHEC có \(\widehat{AHC}=\widehat{AEC}=90^0\)
nên AHEC là tứ giác nội tiếp đường tròn đường kính AC
=>A,H,E,C cùng thuộc đường tròn tâm K, đường kính AC
Xét (K) có
AC là đường kính
AB\(\perp\)AC tại A
Do đó: AB là tiếp tuyến của (K)

Câu hỏi của VRCT_Ran love shinichi - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo tại đây nhé.

a)
Theo đề bài thì DE//BC vì DE và BC đều là tiếp tuyến của đường tròn.
=>Tam giác ADE vuông tại D và tam giác AHC vuông tại H.
=>Hai tam giác vuông này có góc đối bằng nhau: DAE=CAH
Và hai cạnh bằng nhau (là bán kính đường tròn) AD=AH
===> hai tam giác vuông ADE và AHC bằng nhau
===>hai cạnh bằng nhau: AE=AC
Xét tam giác BEC có AE=AC hay gọi được gọi A là trung điểm của EC=> BA là trung tuyến của EBC kẻ từ B
Và tam giác BEC cũng có góc BAC vuông, hay còn gọi là đường cao.
Một tam giác có đường cao cũng là đường trung tuyến vậy tam giác BEC cân tại B
--------------------------------------...
b)
Vì BA vừa là trung tuyến vừa là đường cao của tam giác BEC cho nên BA chia tam giác cân BEC thành hai nửa tam giác vuông, và cũng bằng nhau: BAE=BAC
=> hai đường cao kẻ từ A tới đáy của hai tam giác vuông BAE và BAC là AH và AI phải bằng nhau.
--------------------------------------...
c)
AI= AH= bán kính đường tròn
AI vuông góc với BE theo đề bài
==> BE là tiếp tuyến của đường tròn
--------------------------------------------
