Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Biết AB = 6cm, BC = 5cm, OA = 2cm. Tính CD, AD, AC. Giúp mình nha!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 11 2021
Câu 28. Tổ công tác Covid-19 của bệnh viện Đại học Y Dược gồm 90 bác sĩ và 84 y tá được phân công về 1 huyện để thực hiện xét thần tốc nhằm khoanh vùng dập dịch và điều trị Covid-19 trong các khu cách ly. Muốn phục vụ được nhiều xã hơn, đội dự định chia thành các tổ sao cho số bác sĩ và y tá của các tổ bằng nhau. Hỏi có thể chia được nhiều nhất thành bao nhiêu tổ? Mỗi tổ có mấy bác sĩ, mấy y tá?
A. 12 tổ; 6 bác sĩ và 5 y tá. B. 12 tổ; 5 bác sĩ và 6 y tá.
C. 6 tổ; 15 bác sĩ và 14 y tá. D. 6 tổ; 14 bác sĩ và 15 y tá.
4 tháng 10 2021
Ta có: ABCD là hình bình hành
\(\left\{{}\begin{matrix}CD=AB=8cm\\BC=AD=5cm\end{matrix}\right.\)
Ta có: O là giao điểm 2 đường chéo
\(\Rightarrow AC=2OC=2.3=6\left(cm\right)\)
CM
5 tháng 8 2019
Vì hình bình hành ABCD có 2 cạnh liền kề bằng nhau AB = BC nên ABCD là hình thoi
Suy ra: AB = BC = CD= DA = 10cm và O là trung điểm của AC và trung điểm của BD
Ta có: AC = 2AO = 2. 6 = 12cm
Áp dụng định lí py tago vào tam giác AOD có:
A D 2 = A O 2 + O D 2 suy ra: O D 2 = A D 2 – A O 2 = 10 2 – 6 2 = 64 nên OD = 8cm
Suy ra: BD = 2OD = 16cm
Diện tích hình thoi ABCD là:
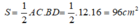
Chọn đáp án A
6 tháng 2 2022
c. -Xét △ADC có: OM//DC (gt).
\(\Rightarrow\dfrac{MO}{DC}=\dfrac{AO}{AC}\) (định lí Ta-let).
\(\Rightarrow\dfrac{DC}{MO}=\dfrac{AC}{AO}\)
\(\Rightarrow\dfrac{DC}{OM}-1=\dfrac{OC}{AO}\) (1).
-Xét △BDC có: ON//DC (gt).
\(\Rightarrow\dfrac{ON}{DC}=\dfrac{BO}{BD}\) (định lí Ta-let).
\(\Rightarrow\dfrac{DC}{ON}=\dfrac{BD}{BO}\)
\(\Rightarrow\dfrac{DC}{ON}-1=\dfrac{OD}{BO}\)
-Xét △ABO có: AB//DC (gt).
\(\Rightarrow\dfrac{OD}{BO}=\dfrac{OC}{OA}=\dfrac{DC}{AB}\) (3)
-Từ (1), (2),(3) suy ra:
\(\dfrac{DC}{OM}-1=\dfrac{DC}{ON}-1=\dfrac{DC}{AB}\)
\(\Rightarrow\dfrac{DC}{OM}=\dfrac{DC}{ON}=\dfrac{DC}{AB}+1=\dfrac{AB+DC}{AB}\)
\(\Rightarrow\dfrac{1}{OM}=\dfrac{1}{ON}=\dfrac{AB+DC}{AB.DC}=\dfrac{1}{AB}+\dfrac{1}{CD}\)
6 tháng 2 2022
a: Xét ΔAOB và ΔCOD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó: ΔAOB∼ΔCOD
Suy ra: \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}\)
hay \(OA\cdot OD=OB\cdot OC\)
b: \(\dfrac{OA}{OC}=\dfrac{AB}{CD}\)
\(\Leftrightarrow OA=\dfrac{1}{2}\cdot6=3\left(cm\right)\)
CM
20 tháng 5 2017
Theo tính chất hình bình hành ta có: I là trung điểm của AC và BD.
Suy ra:
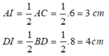
Xét tam giác AID có: A I 2 + I D 2 = A D 2 ( 3 2 + 4 2 = 5 2 = 25 )
Suy ra: tam giác AID là tam giác vuông: AI ⊥ DI hay AC ⊥ BD
Hình bình hành ABCD có 2 đường chéo AC và BD vuông góc với nhau nên là hình thoi.
Suy ra: AB = BC = CD = DA = 5cm
Chọn đáp án B
28 tháng 6 2020
TỰ VẼ HÌNH NHA
a) Xét ΔABO và ΔCOD có:
\(\widehat{ABO}=\widehat{COD}\left(AB//DC\right)\)
\(\widehat{AOB}=\widehat{DOC}\left(đđ\right)\)
=> \(\text{ Δ}ABO~\text{Δ}COD\left(g.g\right)\)
\(\Rightarrow\frac{OA}{OB}=\frac{OC}{OD}\)
\(\Leftrightarrow OA.OD=OB.OC\)
b) vì ΔABO~ΔCOD
=> \(\frac{DC}{OC}=\frac{AB}{OA}\)
\(\Leftrightarrow DC.OA=AB.OC\)
\(\Leftrightarrow10.OA=5.6\)
\(\Leftrightarrow OA=3\left(cm\right)\)
OE thì mk chịu
Ta có : CD=AB=6cm
AD=BC=5cm
Ta có : O là giao điểm của hai đường chéo
AC=2OA=2.2=4
đây nha bạn