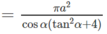Tính S của các hình tam giác trong hình...
Đọc tiếp
Tính S của các hình tam giác trong hình bên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 2 2018
Diện tích hình tam giác AOB là:
9 x 9 : 2 = 40,5 (cm2)
Tích 2 bán kính là:
40,5 x 2 = 81 (cm)
Diện tích của hình tròn là:
81 x 3,14 = 245,34 (cm2)
Đáp số: 245,34 cm2
CM
21 tháng 3 2018
Đáp án C
Cạnh đáy của hình chóp bằng 2 và diện tích một mặt bên bằng nên 2 2 3 4 = 3 nên S t p = 4 + 4 3
CM
20 tháng 7 2019
Đáp án D
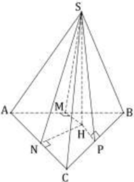
Theo giả thiết, các mặt bên tạo với đáy một góc 45 độ nên hình chiếu vuông góc của S trên (ABC) chính là tâm đường tròn nội tiếp tam giác ABC hay H là tâm đường tròn nội tiếp tam giác ABC.
CM
10 tháng 9 2018
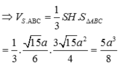
Đáp án D
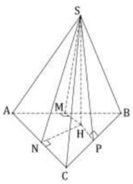
Theo giả thiết, các mặt bên tạo với đáy một góc 45 ° nên hình chiếu vuông góc của S trên (ABC) chính là tâm đường tròn nội tiếp ΔABC hay H là tâm đường tròn nội tiếp ΔABC .
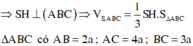
Áp dụng công thức Hê-rông em tính được p = 9 a 2 và S ΔABC = 3 15 a 2 4 .
Em lại có: S ΔABC = p . r với r là bán kính đường tròn nội tiếp tam giác ABC.
Từ H, em kẻ HM, HN, HP lần lượt vuông góc với AB, AC, BC thì
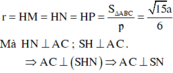
=> Góc giữa (SAC) và (ABC) chính là góc giữa SN và HN hay SNH ⏜ = 45 °
CM
14 tháng 12 2019
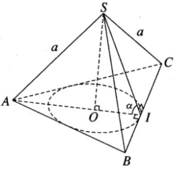
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và ∠ SIO = α. Đặt OI = r, SO = h, ta có AO = 2r và
Do đó a 2 = r 2 tan 2 α + 4 r 2 = r 2 tan 2 α + 4
Vậy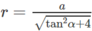 
Hình nón nội tiếp có đường sinh là :
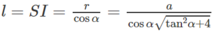
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
