tính chu vi một tam giác biết 3 cạnh tỉ lệ với 7;5;3 và cạnh lớn nhất dài hơn cạnh nhỏ nhất là 12cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 11 2021
\(a,\) Gọi độ dài 3 cạnh là a,b,c(cm;0<a<b<c<120)
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{120}{12}=10\\ \Rightarrow \begin{cases} a=10.3=30\\ b=10.4=40\\ c=10.5=50 \end{cases} \)
Vậy ...
\(b,\) Gọi độ dài 3 cạnh là a,b,c(cm;0<a<b<c)
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{c-a}{7-3}=\dfrac{80}{4}=20\\ \Rightarrow \begin{cases} a=20.3=60\\ b=20.5=100\\ c=20.7=140 \end{cases}\\ \Rightarrow P=a+b+c=300(cm)\)
HB
26 tháng 12 2017
gọi các cạnh cú tam giác đó là a;b;c (>o)(cm)
theo bài ra ta có
a/3=b/5=c/7 và a+b+c=45
áp dụng.....ta có
a/3=b/5=c/7=a+b+c/3+5+7=45/15=3
a/3=3 thì a=9
b/5=3 thì b=15
c/7=3 thì c=21
XO
14 tháng 8 2020
Gọi độ dài 3 cạnh của tam giác lần lượt là a ; b ; c với a < b < c
Ta có : \(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{40,5}{15}=2,7\)(Dãy tỉ số bằng nhau)
=> a = 8,1 ; b = 13,5 ; c = 18,9
Vậy độ dài 3 cạnh tam giác lần lượt là 8,1 cm ; 13,5 cm ; 18,9 cm
VC
Vũ Cao Minh⁀ᶦᵈᵒᶫ ( ✎﹏IDΣΛ亗 )
CTV
VIP
14 tháng 8 2020
Gọi các cạnh tỉ lệ 3 ; 5 ; 7 của tam giác lần lượt là \(a;b;c\left(a;b;c>0\right)\)
Vì các cạnh tỉ lệ với 3 ; 5 ; 7 \(\Rightarrow\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\).
Mà chu vi tam giác bằng 40,5 cm \(\Leftrightarrow a+b+c=40,5\left(cm\right)\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có :
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{40,5}{15}=2,7\)
\(\Leftrightarrow a=2,7.3=8,1\left(cm\right);b=2,7.5=13,5\left(cm\right);c=2,7.7=18,9\left(cm\right)\)
Vậy độ dài các cạnh của tam giác là 8,1 ; 13,5 và 18,9 cm
HA
14 tháng 10 2017
Gọi 3 cạnh của tam giác lần lượt là a, b, c (a,b,c thuộc N sao). Áp dụng tính chất của dãy tỉ số bằng nhau, ta có
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{c-a}{7-3}=\frac{3}{2}\)
\(\frac{a}{3}\)= \(\frac{3}{2}\)=> a = 4.5
\(\frac{b}{5}\)= \(\frac{3}{2}\)=> b = 7.5
\(\frac{c}{7}\)= \(\frac{3}{2}\)=> c = 10.5
Chu vi tam giác: 4.5 + 7.5 + 10.5 = 22.5(cm)
28 tháng 11 2015
gọi độ dài 3 cạnh của tam giác đó lần lượt là x;y;z(x;y;z>0)
ta có :
x/3=y/5=z/7 và x+y+z=150
áp dụng tc dãy ts = nhau ta có :
x/3=y/5=z/7=x+y+z/3+5+7=150/15=10
=>x/3=10=>x=30 cm
=>y/5=10=>y=50 cm
=>z/7=10=>z=70 cm
vậy ...
28 tháng 11 2015
Gọi độ dài ba cạnh là x;y;z
Theo bài ra ta có : \(\frac{x}{3}+\frac{x}{5}+\frac{x}{7}=150\)
Áp dụng dãy tỉ bằng nhau : \(\frac{x}{3}+\frac{x}{5}+\frac{x}{7}=\frac{150}{15}=10\)
\(\Rightarrow\) \(\frac{x}{3}=10\Rightarrow x=30\)
\(\Rightarrow\frac{y}{5}=10\Rightarrow x=50\)
\(\Rightarrow\)\(\frac{z}{7}=10\Rightarrow z=70\)
P/s : Sai đừng trách nha - Bởi mình mới lớp 6
NH
5
10 tháng 9 2016
Gọi 3 cạnh của tam giác lần lượt là x,y,z
Ta có: \(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}\)
Áp dụng tc dãy tỉ
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{x+y+z}{3+5+7}=\frac{35}{15}=\frac{7}{3}\)
\(\begin{cases}\frac{x}{3}=\frac{7}{3}\\\frac{y}{5}=\frac{7}{3}\\\frac{z}{7}=\frac{7}{3}\end{cases}\)\(\Rightarrow\begin{cases}x=7\\y=\frac{35}{3}\\z=\frac{49}{3}\end{cases}\)
10 tháng 9 2016
Gợi 3 cạnh của tam giác lần lượt là a,b,c
Theo đề bài ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\) và a+b+c=35
Áp dụng tính chất của dãy tỉ ssoos bằng nhau ta cd:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{35}{15}=\frac{7}{3}\)
=>\(\begin{cases}a=7\\b=\frac{35}{3}\\c=\frac{49}{3}\end{cases}\)
2 tháng 10 2021
chu vi tam giác là 30x2=60
gọi 3 cạnh lần lượt là a;b;c
ta có a/3=b/4=c/5
=>a+b+c/3+4+5=60/12=5
=>a=5x3=15
b=5x4=20
c=5x5=25
đây nhé
N
15 tháng 11 2021
1. Áp dụng TCDTSBN:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{a+b}{3+5}=\dfrac{32}{8}=4\)
\(\Rightarrow\left\{{}\begin{matrix}a=12\\b=20\end{matrix}\right.\)
15 tháng 11 2021
1. Áp dụng t/c dtsbn ta có:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{a+b}{3+5}=\dfrac{32}{8}=4\)
\(\dfrac{a}{3}=4\Rightarrow a=12\\ \dfrac{b}{5}=4\Rightarrow b=20\)
2. gọi độ dài 3 cạnh tam giác lần lượt là a,b,c
Ta có: \(\left\{{}\begin{matrix}\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{c}{9}\\a+b+c=630\left(m\right)\end{matrix}\right.\)
Áp dụng t/c dtsbn ta có:
\(\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{c}{9}=\dfrac{a+b+c}{5+7+9}=\dfrac{630}{21}=30\left(m\right)\)
\(\dfrac{a}{5}=30\Rightarrow a=150\left(m\right)\\ \dfrac{b}{7}=30\Rightarrow b=210\left(m\right)\\ \dfrac{c}{9}=30\Rightarrow c=270\left(m\right)\)
CM
23 tháng 12 2017
Gọi chiều dài của các cạnh của tam giác tỉ lệ với 2 ,3 ,4 (cm) lần lượt là x ,y ,z
Các cạnh của tam giác tỉ lệ với 2, 3, 4 nghĩa là x : 2 = y : 3 = z : 4, hay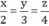 
Chu vi tam giác bằng 45 nghĩa là x + y+ z = 45
Theo tính chất của dãy tỉ số bằng nhau ta có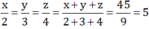 
Do đó x = 5.2 = 10 ; y = 5.3 = 15 ; z = 5.4 = 20
Vậy các cạnh của tam giác là 10cm ; 15cm ; 20cm
CM
17 tháng 5 2019
Gọi độ dài các cạnh của tam giác lần lượt là x, y, z
Theo đề bài ta có: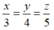 
và x + y + z = 36
Theo tính chất của dãy tỉ số bằng nhau ta có:
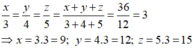
Chọn đáp án A
gọi ba cạnh của tam giác lần lượt là a, b, c, với a,b,c thuộc n*:
ta có: a/7 = b/5 = c/3 mà cạnh lớn nhất dài hơn cạnh nhở nhất 12cm
áp dụng tính chất dãy tỉ số bằng nhau, ta có:
a/7 = b/5 = c/3 = a-c/7-3 = 12/4 = 3
a/7 = 3 => a = 3x7=21
b/5 = 3 => b = 5x3=15
c/3 = 3 => c = 3x3 =9
học tốt nha