Cho x+y=4 và x2+y2=10. Khi đó xy bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x+y=4\\ \Leftrightarrow\left(x+y\right)^2=16\\ \Leftrightarrow x^2+y^2+2xy=16\\ \Leftrightarrow10+2xy=16\\ \Leftrightarrow2xy=6\\ \Leftrightarrow xy=3\)

Vũ Việt Anh ukm, pn cx zậy nha^^^^^^^^^ hihi ^_^

Đáp án A
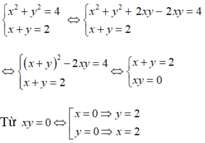
Vậy hệ phương trình có hai nghiệm (x; y) = (0; 2); (x; y) = (2; 0) Từ giả thiết x > y nên x = 2; y = 0 ⇒ xy = 0

a: \(=\left(x-y\right)\left(x+y\right)\)
\(=74\cdot100=7400\)
c: \(=\left(x+2\right)^3\)
\(=10^3=1000\)
a) \(=\left(x-y\right)\left(x+y\right)\)
Thay \(x=87;y=13\) ta đc: \(\left(87-13\right)\left(87+13\right)=74\cdot100=7400\)
b)\(=\left(x-y\right)\left(x^2+xy+y^2\right)=x^3-y^3\)
Thay \(x=10;y=-1\) ta đc:
\(10^3-\left(-1\right)^3=1000-1=999\)
c)\(=\left(x+2\right)^3\)
Thay \(x=8\) ta đc: \(\left(8+2\right)^3=10^3=1000\)
d)\(=x^2-8x+16+1=\left(x-4\right)^2+1\)
Thay \(x=104\) ta đc: \(\left(104-4\right)^2+1=100^2+1=10001\)

Vì x và y là hai đại lượng tỉ lệ nghịch nên:
\(\frac{x_1}{x_2}=\frac{y_2}{y_1}\) hay \(\frac{-3}{2}=\frac{y_2}{y_1}\)hay \(\frac{y_1}{2}=\frac{y_2}{-3}\)
Mặc khác có: y1 - y2 = 13
Áp dụng t/c dãy t/s bằng nhau, ta có:
\(\frac{y_2}{-3}=\frac{y_1}{2}=\frac{y_1-y_2}{-3-2}=\frac{13}{-5}\)
\(\frac{y_2}{-3}=5\Rightarrow y_2=-15;\frac{y_1}{2}=5\Rightarrow y_1=10\)
Khi đó xy = -3 . 10 = -30

a: \(A=x^2+y^2=\left(x+y\right)^2-2xy=15^2-2\cdot50=115\)
c: \(x-y=\sqrt{\left(x+y\right)^2-4xy}=\sqrt{15^2-4\cdot50}=5\)
\(C=x^2-y^2=\left(x+y\right)\left(x-y\right)=15\cdot5=75\)

a: \(A=x^2+y^2=\left(x+y\right)^2-2xy=15^2-2\cdot50=125\)
b:\(B=x^4+y^4\)
\(=\left(x^2+y^2\right)^2-2x^2y^2\)
\(=125^2-2\cdot2500\)
=10625
c: \(x-y=\sqrt{\left(x+y\right)^2-4xy}=\sqrt{15^2-4\cdot50}=5\)
\(C=x^2-y^2=\left(x-y\right)\left(x+y\right)=15\cdot5=75\)

Ta có \(\left(x+y\right)^2=x^2+2xy+y^2\)
Vì \(\hept{\begin{cases}x+y=4\\x^2+y^2=10\end{cases}}\)\(\Rightarrow4^2=10+2xy\Leftrightarrow2xy=6\Leftrightarrow xy=3\)
Vậy \(xy=3\)
Ta có : \(xy=\frac{\left(x+y\right)^2-\left(x^2+y^2\right)}{2}=\frac{4^2-10}{2}=3\)