Cho đường thẳng b song song với đường thẳng c. Đường thẳng d cắt đường thẳng b và c lần lượt tại điểm B và C. Biết rằng ^B3 = 90°.
Số đo góc ^C1 = bao nhiêu°
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kết quả góc = 80 nhé.
Xem thêm tại đây: https://www.facebook.com/groups/giaibaitaponline/permalink/593408784151858/?comment_id=593410360818367¬if_t=group_comment¬if_id=1464852917725746

Ta có:
\(\widehat{D_1}-\widehat{D_2}=4^0\Rightarrow\widehat{D_1}=4+\widehat{D_2}\) (1)
Ta lại có: \(\widehat{D_1}+\widehat{D_2}=180^0\) (2)
thế (1) vào (2), ta được:
\(\widehat{D_1}+\widehat{D_2}=180^0\)
\(\Rightarrow4^0+\widehat{D_2}+\widehat{D_2}=180^0\)
\(\Rightarrow4+2.\widehat{D_2}=180^0\)
\(\Rightarrow\widehat{D_2}=88^0\)
\(\Rightarrow\widehat{D_1}=88+4=92^0\)
\(\Rightarrow\widehat{E_4}=92^0\)
Do góc D1-D2=4 dộ
Mà D1+D2=180 độ
=> D1=92 độ
Vì D1=EDb=92 độ( đối đỉnh)
Mà c//b=> EDb=E4=92 độ
Đáp số : ^E4=92 độ

(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
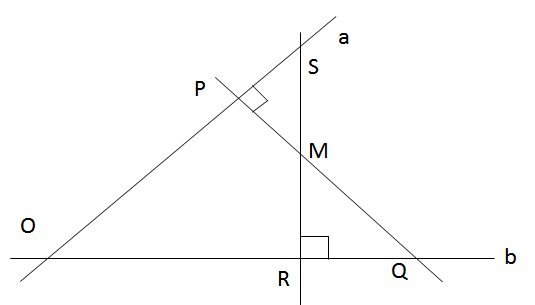
(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b

Gọi A là giao điểm của a và b.
Theo giả thiết c ⟘ a hay SR ⟘ AQ hay SR là đường cao của ΔASQ.
d ⟘ b hay PQ ⟘ AS hay QP là đường cao của ΔASQ.
SR cắt QP tại M ⇒ M là trực tâm của ΔASQ
⇒ AM ⟘ SQ
Vậy đường thẳng đi qua M và vuông góc với SQ cũng đi qua A (đpcm).
bn vẽ hình ms biết ^B3 ở đâu chứ?
vì ^C1 sole trong với ^B3 (b//c,d cắt b và c) nên ^C1=^B3=90 độ