Ta xét các hình vuông có cạnh dài 1 mét. Hỏi ta cần bao nhiêu hình vuông để tạo thành một hình vuông gấp chu vi gấp 4000 lần cạnh hình vuông đơn vị ?
Số hình vuông đơn vị tạo là : ...........
Giúp tớ nha !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 2 2018
Gọi số cạnh hình vuông là ƯCLN (90,50)
90=3^2 .2.5
50=5^2.2
ƯCLN(90,50)=2.5=10
Cách chia: xem như cạnh đó là một ƯCLN
Cạnh đó =10cm
29 tháng 8 2017
Gọi a là cạnh của hình vuông.
Do 108 chia hết cho a, 42 chia hết cho a ⇒a là UC của 108 và 42
Vì a là lớn nhất ⇒a = UCLN ( 108, 42 ) = 6
Vậy cạnh của hình vuông là 6 ( m )
Chúc bạn luôn luôn học giỏi
21 tháng 8 2017
Gọi a là cạnh của hình vuông.
Do 108 chia hết cho a, 42 chia hết cho a \(\Rightarrow\)a là UC của 108 và 42
Vì a là lớn nhất \(\Rightarrow\)a = UCLN ( 108, 42 ) = 6
Vậy cạnh của hình vuông là 6 ( m )
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a) \({S_n} = {5^n}.{\left( {\frac{1}{{{3^n}}}} \right)^2} = {5^n}.\frac{1}{{{9^n}}} = {\left( {\frac{5}{9}} \right)^n},n = 1,2,3,...\)
\(\lim {S_n} = \lim {\left( {\frac{5}{9}} \right)^n} = 0\)
b) \({p_n} = {5^n}.4.\frac{1}{{{3^n}}} = 4.{\left( {\frac{5}{3}} \right)^n},n = 1,2,3,...\)
\(\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right)\)
Vì \(\lim \frac{1}{{4.{{\left( {\frac{5}{3}} \right)}^n}}} = \frac{1}{4}.\lim {\left( {\frac{3}{5}} \right)^n} = 0\) và \(4.{\left( {\frac{5}{3}} \right)^n} > 0\) với mọi \(n\) nên \(\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right) = + \infty \).
AH
Akai Haruma
Giáo viên
30 tháng 6
Lời giải:
a. Gọi $x$ (m) là độ dài cạnh hình vuông được chia ($x\in\mathbb{N}$)
Theo đề ra, $x$ là $ƯC(105,75)$
Để $x$ lớn nhất thì $x=ƯCLN(105,75)$
$\Rightarrow x=15$ (m)
b.
Diện tích thửa đất: $105\times 75=7875$ (m2)
Diện tích mỗi ô vuông đất: $15\times 15=225$ (m2)
Số thửa đất ô vuông là: $7875:225=35$ (ô)
28 tháng 11 2021
Chu vi hình vuông khi gấp đôi đoạn AB là:
36⋅4⋅3⋅2:4=216(cm)
3 tháng 10 2021
Chu vi hình vuông khi gấp đôi đoạn AB là:
\(36\cdot4\cdot3\cdot2:4=216\left(cm\right)\)
CM
8 tháng 9 2017
Chọn B
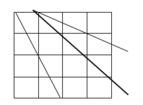
Số cách chọn ra 3 đỉnh trong số 25 đỉnh của các hình vuông đơn vị là: C 25 3
TH1: 3 đỉnh nằm trên cùng 1 hàng hoặc cùng 1 cột là: 5 C 5 3 + 5 C 5 3
TH2: 3 đỉnh nằm trên một trong các đường chéo của hình vuông kích thước 4x4, 3x3, 2x2 sao cho các đường chéo ấy không trùng nhau là 
TH3: 3 đỉnh nằm trên một trong các đường chéo của hình chữ nhật kích thước 2x4. Số hình chữ nhật đó là 6. Do đó số cách chọn là 12
Vậy số tam giác được tạo thành là 
= 2148
Chu vi hình vuông đơn vị là:
\(1\times4=4\left(m\right)\)
Chu vi hình vuông lớn là:
\(4\times4000=16000\left(m\right)\)
Độ dài cạnh hình vuông lớn là:
\(16000\div4=4000\left(m\right)\)
Số hình vuông đơn vị tạo là:
\(4000\div1=4000\)(hình)