Cho đường tròn tâm O bán kính 1 cm và 100 điểm bất kì nằm trên mặt phẳng đường tròn.
CMR: Tồn tại 1 điểm M nằm trên đường tròn mà tổng khoảng cách từ M đến 100 điểm đx cho không nhỏ hơn 100
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 2 2016
Khó quá trời Tui học lớp 8 cũng chưa làm ra
Mà hình như cái này là của lớp 9 mà
VT
20 tháng 1 2019
Đáp án D
- S chuyển động tròn đều trên đường tròn tâm O bán kính 5cm với tốc độ góc 10π (rad/s)
- Vật m dao động điều hoà với với:
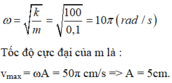
- Tại thời điểm nào đó, điểm sáng S đang đi qua vị trí như trên hình vẽ, còn vật nhỏ m đang có tốc độ cực đại (m có tốc độ cực đại khi qua vị trí cân bằng) => S và m luôn lệch pha nhau góc π/2.
S và m cách nhau lớn nhất khi m và S đi xung quanh vị trí cân bằng. Biểu diễn trên đường tròn lượng giác ta có:
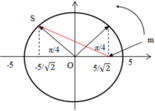
Áp dụng định lí Py – ta – go, ta có khoảng cách lớn nhất giữa S và m (đường màu đỏ) là:
VT
19 tháng 7 2018
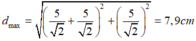
- S chuyển động tròn đều trên đường tròn tâm O bán kính 5cm với tốc độ góc 10π (rad/s)
- Vật m dao động điều hoà với với:
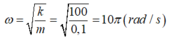
Tốc độ cực đại của m là : vmax = ωA = 50π cm/s => A = 5cm.
- Tại thời điểm nào đó, điểm sáng S đang đi qua vị trí như trên hình vẽ, còn vật nhỏ m đang có tốc độ cực đại (m có tốc độ cực đại khi qua vị trí cân bằng) => S và m luôn lệch pha nhau góc π/2.
S và m cách nhau lớn nhất khi m và S đi xung quanh vị trí cân bằng. Biểu diễn trên đường tròn lượng giác ta có :
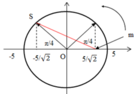
Áp dụng định lí Py – ta – go, ta có khoảng cách lớn nhất giữa S và m (đường màu đỏ) là :
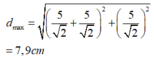
Đáp án D
VT
8 tháng 5 2018
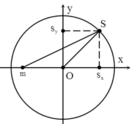
Chọn gốc thời gian là khi trạng thái dao động của hệ như hình vẽ → phương trình dao động của vật và hình chiếu của S theo phương ngang Ox là:
27 tháng 9 2015
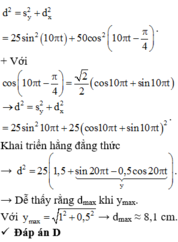
Nếu khoảng cách giữa hai điểm bất kì đều bé hơn 1 thì ta chỉ cần chọn 1 điểm \(A\) bất kì trong số 2001 điểm đã cho, rồi vẽ đường tròn \(\left(A,1\right)\), đường tròn này sẽ chứa cả 2000 điểm còn lại, do đó ta có đpcm.
Gỉa sử rằng có hai điểm \(A,B\) trong số 2001 điểm đã cho mà có khoảng cách lớn hơn \(1\). Vẽ các đường tròn tâm là \(A,B\) và bán kính cùng là \(1\). Ta còn lại 1999 điểm. Mỗi điểm \(C\) bất kì trong số 1999 điểm ấy, theo giả thiết \(AB,AC,BC\) phải có một đoạn có độ dài bé hơn \(1\). Vì \(AB>1\) nên \(AC
18 tháng 10 2023
a: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của \(\widehat{MOA}\left(1\right)\)
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của \(\widehat{MOB}\)(2)
Từ (1), (2) suy ra \(\widehat{COD}=\widehat{COM}+\widehat{DOM}\)
\(=\dfrac{1}{2}\left(\widehat{MOA}+\widehat{MOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
=>ΔCOD vuông tại O
b: AC+BD
=CM+MD
=CD
c:
Xét ΔCOD vuông tại O có OM là đường cao
nên \(CM\cdot MD=OM^2\)
=>\(CA\cdot BD=R^2\) không đổi