Tìm tập xác định của mỗi hàm số sau:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì -1 ≤ sinx ≤ 1 nên 3 - sinx > 0 với mọi x nên tập xác định của hàm số là D = R.
b) y = (1 - cosx)/sinx xác định khi và chỉ khi sinx ≠ 0
⇔ x ≠ kπ, k ∈ Z.
Vậy tập xác định D = R\{kπ|k ∈ Z}
c) Vì 1 - sinx ≥ 0 và 1 + cosx ≥ 0 nên hàm số xác định khi và chỉ khi
cosx ≠ -1 ⇔ x ≠ π + k2π, k ∈ Z.
Vậy tập xác định D = R\{π + k2π|k ∈ Z}

a) Biểu thức \(2x + 3\) có nghĩa với mọi x, nên có tập xác định \(D = \mathbb{R}\)
Do đó tập giá trị của hàm số là \(\mathbb{R}\)
b) Biểu thức \(2{x^2}\) có nghĩa với mọi x, nên có tập xác định \(D = \mathbb{R}\)
Ta có: \({x^2} \ge 0\) Do đó \(y = 2{x^2} \ge 0\), tập giá trị của hàm số là \(\left[ {0; + \infty } \right)\)

Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .

Hàm số xác định khi \(sin\left(\dfrac{x}{2}-\dfrac{\pi}{3}\right)\ne0\)
\(\Leftrightarrow\dfrac{x}{2}-\dfrac{\pi}{3}\ne k\pi\)
\(\Leftrightarrow\dfrac{x}{2}\ne\dfrac{\pi}{3}+k\pi\)
\(\Leftrightarrow x\ne\dfrac{2\pi}{3}+k2\pi\left(k\in Z\right)\)

\(y=\sqrt[]{1-sinx}\) xác định \(\Leftrightarrow1-sinx\ge0\)
\(\Leftrightarrow sinx\le1\left(luôn.đúng\right)\)
\(\Leftrightarrow\forall x\in R\)

Do \(9x^2+6x+5=\left(3x+1\right)^2+4>0;\forall x\) nên hàm xác định trên R

a) Hàm số xác định khi x 2 − 4x + 3 ≠ 0 hay x ≠ 1; x ≠ 3.
Vậy tập xác định của hàm số đã cho là R \ {1;3}.
b) Hàm số xác định khi x 3 – 8 > 0 hay x > 2. Vậy tập xác định là (2; + ∞ ).
c) Hàm số xác định khi x 3 – 3 x 2 + 2x > 0 hay x(x – 1)(x – 2) > 0
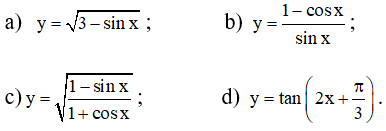
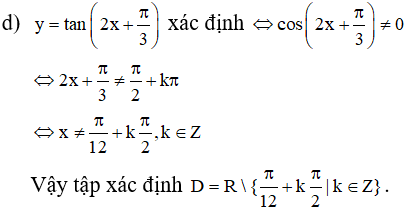

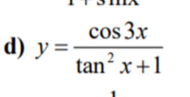 tìm tập xác định của hàm số sau
tìm tập xác định của hàm số sau 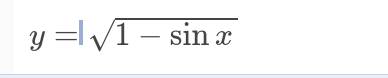
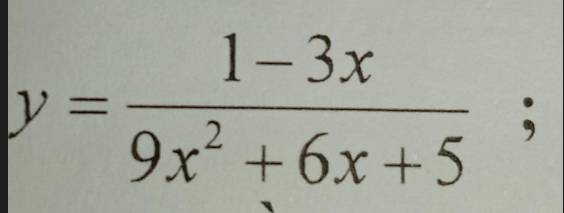
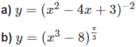
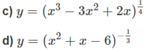
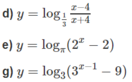
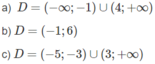
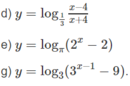
a) Vì -1 ≤ sinx ≤ 1 nên 3 - sinx > 0 với mọi x nên tập xác định của hàm số là D = R.
b) y = (1 - cosx)/sinx xác định khi và chỉ khi sinx ≠ 0
⇔ x ≠ kπ, k ∈ Z.
Vậy tập xác định D = R\{kπ|k ∈ Z}
c) Vì 1 - sinx ≥ 0 và 1 + cosx ≥ 0 nên hàm số xác định khi và chỉ khi
cosx ≠ -1 ⇔ x ≠ π + k2π, k ∈ Z.
Vậy tập xác định D = R\{π + k2π|k ∈ Z}
a, \(D=R\)