cho tam giác ABC (AB<AC), các phân giác BD,CE
a, đường thẳng qua D và song song với BC cắt AB ở K. Chứng minh rằng E nằm giữa B và K
b, Chứng minh rằng CD>DE>BE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 6 2023
góc AEB=góc ADB=90 độ
=>AEDB nội tiếp
góc CDH+góc CEH=180 độ
=>CEHD nội tiếp
8 tháng 3 2021
Xét tứ giác DHEC có
\(\widehat{HDC}\) và \(\widehat{HEC}\) là hai góc đối
\(\widehat{HDC}+\widehat{HEC}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: DHEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
25 tháng 1
a: Xét tứ giác BDHF có \(\widehat{BDH}+\widehat{BFH}=90^0+90^0=180^0\)
=>BDHF là tứ giác nội tiếp
Xét tứ giác AFDC có \(\widehat{AFC}=\widehat{ADC}=90^0\)
nên AFDC là tứ giác nội tiếp
Sửa đề; CEHD
Xét tứ giác CEHD có
\(\widehat{CEH}+\widehat{CDH}=90^0+90^0=180^0\)
=>CEHD là tứ giác nội tiếp
Xét tứ giác ABDE có \(\widehat{AEB}=\widehat{ADB}=90^0\)
nên ABDE là tứ giác nội tiếp
b: Ta có: \(\widehat{FDH}=\widehat{FBH}\)(FBDH là tứ giác nội tiếp)
\(\widehat{EDH}=\widehat{ECH}\)(ECDH là tứ giác nội tiếp)
mà \(\widehat{FBH}=\widehat{ECH}\left(=90^0-\widehat{FAC}\right)\)
nên \(\widehat{FDH}=\widehat{EDH}\)
=>DH là phân giác của góc EDF
CM
30 tháng 1 2017
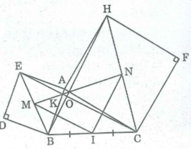
* Trong ∆ EBC , ta có: M là trung điểm EB (tính chất hình vuông)
I trung điểm BC (gt)
Nên MI là đường trung bình của ΔEBC
⇒ MI = 1/2 EC và MI // EC (tính chất đường trung bình của tam giác).
Trong ∆ BCH, ta có: I trung điểm BC (gt)
N trung điểm của CH (tính chất hình vuông)
Nên NI là đường trung bình của ∆ BCH
⇒ NI = 1/2 BH và NI // BH (tính chất đường trung bình của tam giác)
Mà BH = CE (chứng minh trên)
Suy ra: MI = NI nên ∆ INM cân tại I
MI // EC (chứng minh trên)
EC ⊥ BH (chứng minh trên)
Suy ra: MI ⊥ BH. Mà NI // BH (chứng minh trên)
Suy ra: MI ⊥ NI hay ∠ (MIN) = 90 0
Vậy ∆ MIN vuông cân tại I.
13 tháng 6 2023
a: góc AEB=góc ADB=90 độ
=>AEDB nội tiếp
b,c: M ở đâu vậy bạn?
13 tháng 3 2022
Xét tứ giác ABDE:
\(\widehat{AEB}=90^o\left(AE\perp BE\right).\\ \widehat{ADB}=90^o\left(AD\perp BD\right).\\ \Rightarrow\widehat{AEB}=\widehat{ADB}.\)
Mà 2 đỉnh E, D kề nhau, cùng nhìn cạnh AB.
\(\Rightarrow\) Tứ giác ABDE nội tiếp (dhnb).
Xét tứ giác HDCE:
\(\widehat{HEC}=90^o\left(DE\perp EC\right).\\ \widehat{HDC}=90^o\left(HD\perp DC\right).\\ \Rightarrow\widehat{HEC}+\widehat{HDC}=180^o.\)
Mà 2 góc này ở vị trí đối nhau.
\(\Rightarrow\) Tứ giác HDCE nội tiếp (dhnb).
Tứ giác ABDE nội tiếp (cmt).
\(\Rightarrow\widehat{EBD}=\widehat{BAD}.\)
Xét \(\Delta DBH\) và \(\Delta DAC:\)
\(\widehat{BDH}=\widehat{ADC}\left(=90^o\right).\)
\(\widehat{HBD}=\widehat{CAD}\left(\widehat{EBD}=\widehat{BAD}\right).\)
\(\Rightarrow\Delta DBH\sim\Delta DAC\left(g-g\right).\)
\(\Rightarrow\dfrac{DB}{DA}=\dfrac{DH}{DC}.\\ \Rightarrow DB.DC=DH.DA.\)
moi hok lop 6
minh h lop 5