tìm giá trị nguyên của n để 6n-5 chia hết cho 3n+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
1
20 tháng 2 2021
6n-5 chia hết cho 3n-1
mà 6n-5=3(3n-1)-8
vậy 3n-1 thuộc Ư(8)=(-1;1;-2;2;-4;4;-8;8)
| 3n-1 | -1 | 1 | -2 | 2 | -4 | 4 | -8 | 8 |
| n | 0 | L | L | 1 | -1 | L | L | 3 |
vậy n thuộc (0;1;-1;3)
k cho mik zới
B
1
AH
Akai Haruma
Giáo viên
4 tháng 10
Lời giải:
$6n-3\vdots 1-3n$
$\Rightarrow -1-2(1-3n)\vdots 1-3n$
$\Rightarrow -1\vdots 1-3n$
$\Rightarrow 1-3n\in \left\{1; -1\right\}$
$\Rightarrow n\in \left\{0; \frac{2}{3}\right\}$
Vì $n$ nguyên nên $n=0$
HV
3
6 tháng 1 2023
a: =>\(n+2\in\left\{1;-1;7;-7\right\}\)
=>\(n\in\left\{-1;-3;5;-9\right\}\)
b: =>n-3+4 chia hết cho n-3
=>\(n-3\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{4;2;5;1;7;-1\right\}\)
c: =>3n^3+n^2+9n^2-1-4 chia hết cho 3n+1
=>\(3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{0;-\dfrac{2}{3};\dfrac{1}{3};-1;1;-\dfrac{5}{3}\right\}\)
d: =>10n^2-10n+11n-11+1 chia hết cho n-1
=>\(n-1\in\left\{1;-1\right\}\)
=>\(n\in\left\{2;0\right\}\)
TM
3
KN
3 tháng 8 2016
A = (3n^3 + 10n^2 - 5)/(3n + 1)
A = (3n^3 + n^2 + 9n^2 + 3n - 3n - 1 -4)/(3n+1)
A= n^2 + 3n - 1 - 4/(3n+1)
biểu thức 3n^3 + 10n^2 - 5 chia hết cho giá trị của biểu thức 3n + 1 khi:
3n+1 = ±1,±2, ±4
=> n = 0,-2/3,1/3,-1,1,-5/3
chọn giá trị nguyên: n = 0,-1,1
CHÚC BẠN HỌC TỐT
3 tháng 8 2016
\(A=\frac{\left(3n^3+10n^2-5\right)}{\left(3n+1\right)}\)
\(A=\frac{\left(3n^3+n^2+9n^2+3n-3n-1-4\right)}{\left(3n+1\right)}\)
\(A=\frac{n^2+3n-1-4}{\left(3n+1\right)}\)
Biểu thức \(3n^3+10n^2-5\)chia hết cho giá trị của biểu thức \(3n+1\) khi:
3n+1 = ±1,±2, ±4
\(\Rightarrow n=0;-\frac{2}{3};-\frac{1}{3};-1;-\frac{5}{3}\)
Chọn giá trị nguyên:\(n=0;-1;1\)
20 tháng 5 2016
a) Cho 3n +1=0 => n=\(\frac{-1}{3}\)
Sau đó thay vào biểu thức 3n3+10n2-5 sẽ tìm ra n=-4
b) Cho n-1=0 => n=1
Sau đó thay vào biểu thức 10n2+n -10 sẽ tìm ra n=1
Cho mình nha!!! <3
CM
22 tháng 5 2019
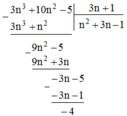
Ta có: 3 n 3 + 10 n 2 - 5 = 3 n + 1 n 2 + 3 n - 1 - 4
Để phép chia đó là chia hết thì 4 ⋮ 3n + 1⇒ 3n + 1 ∈ Ư(4)
3n + 1 ∈ {-4; -2; -1; 1; 2; 4}
3n + 1 = -4⇒ 3n = -5⇒ n =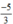 
∉ Z : loại
3n + 1 = -2⇒ 3n = -3⇒ n = -1 ∈ Z
3n + 1 = -1⇒ 3n = -2⇒ n =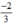 
∉ Z : loại
3n + 1 = 1⇒ 3n = 0⇒ n = 0 ∈ Z
3n + 1 = 2⇒ 3n = 2⇒ n =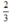 
∉ Z : loại
3n + 1 = 4⇒ 3n = 3⇒ n = 1 ∈ Z
Vậy n ∈ {-1; 0; 1} thì 3 n 3 + 10 n 2 - 5 chia hết cho 3n + 1.
21 tháng 10 2015
Lấy 3n^3 + 10n^2 - 5 : 3n + 1 như bình thường, cuối cùng được dư bao nhiêu thì số đó phải chia hết cho 3n + 1. Thì 3n + 1 phải thuộc tập hợp ước của số đó. Và cứ thế tìm n thôi.
8 tháng 11 2021
1: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;4;2;-2;-1;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;3;-3\right\}\)
hay \(n\in\left\{0;1;-1\right\}\)
6n-5 \(⋮\) 3n+1
\(\Rightarrow\)6n+2-7 \(⋮\) 3n+1
\(\Rightarrow\)2(3n+1)-7\(⋮\)3n+1
\(\Rightarrow\)(3n+1) - 7\(⋮\)3n+1
\(\Rightarrow\)3n+1\(⋮\)3n+1
7\(⋮\)3n+1
\(\Rightarrow\)3n+1 \(\in\)Ư(7) = {-7;-1;1;7}
Lập bảng
3n+1 | -7 | -1 | 1 | 7 |
n | ko có | ko có | 0 | 2 |
\(\Rightarrow\)n \(\in\){0;2}
*Viết xong muốn gãy tay :v*
Để \(6n-5⋮3n+1\)(ĐK : \(n\in Z\))
\(\Leftrightarrow6n+2-7⋮3n+1\)
\(\Leftrightarrow2\left(3n+1\right)-7⋮3n+1\)
\(\Leftrightarrow7⋮3n+1\)
\(\Leftrightarrow3n+1\inƯ_{\left(7\right)}\)
\(\Leftrightarrow3n+1\in\left\{1;-1;7;-7\right\}\)
Ta có bảng :
Vậy S={0;2} thì 6n-5 chia hết cho 3n+1