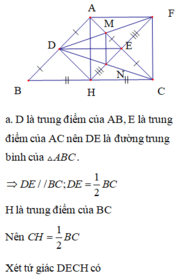
Cho tam giác ABC. Gọi E,F lần lượt là trung điểm của các đoạn thẳng AC và AB. M là điểm tùy ý trên cạnh BC. K là điểm đối xứng với M qua E.
1. Chứng minh tứ giác AMCK là hình bình hành.
2. Chứng minh EF đi qua trung điểm Q của AM.
3. Gọi I là điểm đối xứng với Q qua M. Chứng minh khi M di chuyển thì I luôn di chuyển trên một đường thẳng cố định

.png)