Mn giúp tôi với

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



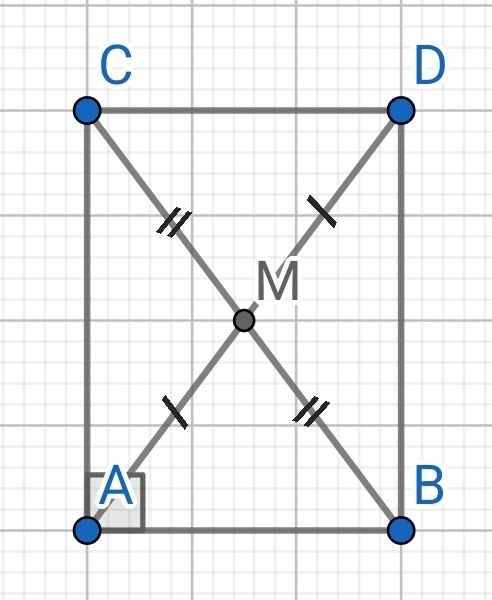
a) Do AM là đường trung tuyến của ∆ABC
⇒ M là trung điểm BC
Do MA = MD (gt)
⇒ M là trung điểm AD
Tứ giác ABDC có:
M là trung điểm BC (cmt)
M là trung điểm AD (cmt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (gt)
⇒ ABDC là hình chữ nhật
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC của ∆ABC
⇒ AM = BC : 2
= 10 : 2
= 5 (cm)
c) Nếu ∠B = 45⁰
⇒ C = 90⁰ - ∠B
= 90⁰ - 45⁰
= 45⁰
⇒ ∆ABC vuông cân tại A
⇒ AB = AC
Lại có ABDC là hình chữ nhật
⇒ ABDC là hình vuông

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)

Lời giải:
$x+y+z=0\Rightarrow x+y=-z$. Khi đó:
$x^2+y^2-z^2=(x+y)^2-2xy-z^2=(-z)^2-2xy-z^2=-2xy$
Tương tự: $y^2+z^2-x^2=-2yz, z^2+x^2-y^2=-2xz$
Khi đó:
$A=\frac{xy}{-2xy}+\frac{yz}{-2yz}+\frac{zx}{-2zx}=\frac{1}{-2}+\frac{1}{-2}+\frac{1}{-2}=\frac{-3}{2}$

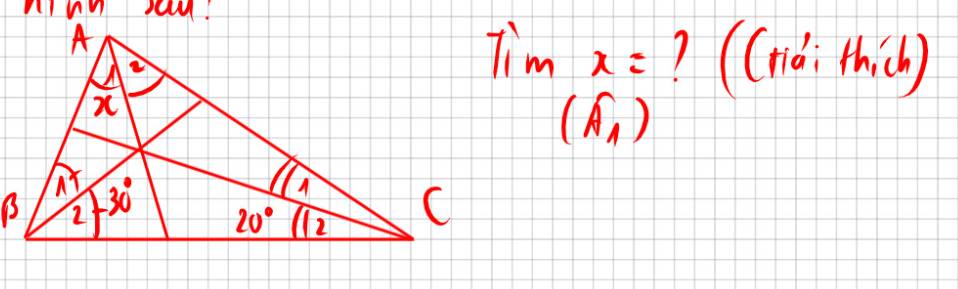
Vẽ lại hình:
Theo hình vẽ, ta có: AH,BH,CH lần lượt là phân giác của góc BAC, góc ABC, góc ACB
BH là phân giác của góc ABC
=>\(\widehat{ABC}=2\cdot\widehat{HBC}=60^0\)
CH là phân giác của góc ACB
=>\(\widehat{ACB}=2\cdot\widehat{HCB}=2\cdot20^0=40^0\)
Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{BAC}+60^0+40^0=180^0\)
=>\(\widehat{BAC}=80^0\)
AH là phân giác của góc BAC
=>\(\widehat{BAH}=\widehat{CAH}=\dfrac{80^0}{2}=40^0\)
=>\(x=40^0\)

Bài 1
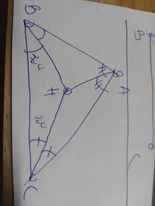
 a) Do AM là đường trung tuyến của ∆ABC
a) Do AM là đường trung tuyến của ∆ABC
⇒ M là trung điểm BC
Do MA = MD (gt)
⇒ M là trung điểm AD
Tứ giác ABDC có:
M là trung điểm BC (cmt)
M là trung điểm AD (cmt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (gt)
⇒ ABDC là hình chữ nhật
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC của ∆ABC
⇒ AM = BC : 2
= 10 : 2
= 5 (cm)
c) Nếu ∠B = 45⁰
⇒ C = 90⁰ - ∠B
= 90⁰ - 45⁰
= 45⁰
⇒ ∆ABC vuông cân tại A
⇒ AB = AC
Lại có ABDC là hình chữ nhật
⇒ ABDC là hình vuông
Bài 2
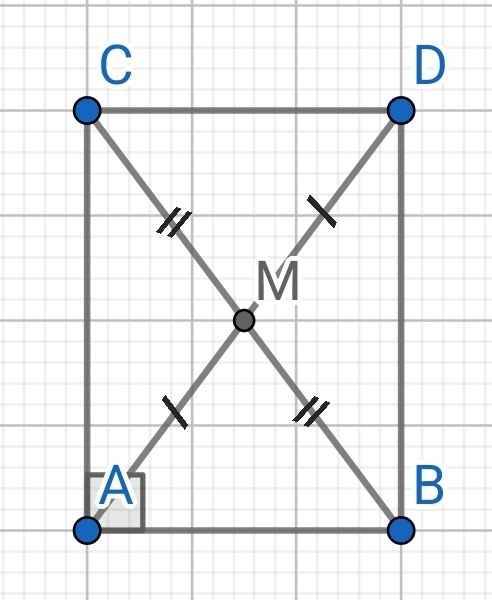
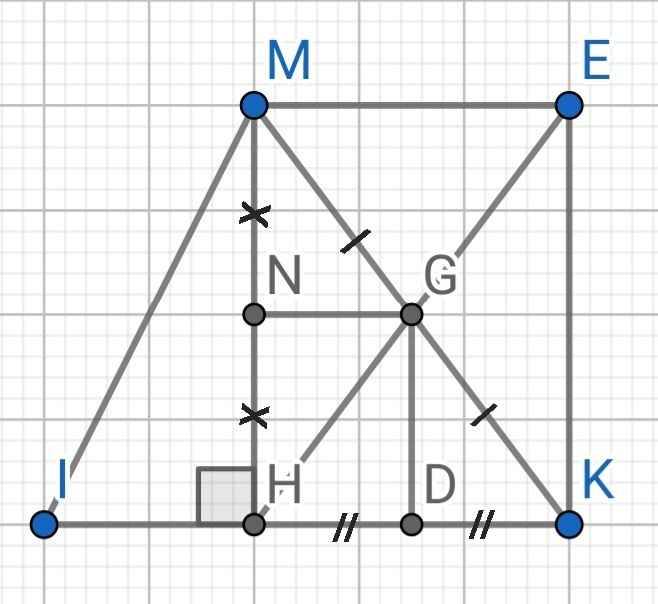 a) Do H và E đối xứng với nhau qua G (gt)
a) Do H và E đối xứng với nhau qua G (gt)
⇒ G là trung điểm của HE
Tứ giác MEKH có:
G là trung điểm HE (cmt)
G là trung điểm MK (gt)
⇒ MEKH là hình bình hành
Mà ∠MHK = 90⁰ (MH ⊥ IK)
⇒ MEKH là hình chữ nhật
b) ∆MHK có:
N là trung điểm MH (gt)
G là trung điểm MK (gt)
⇒ NG là đường trung bình của ∆MHK
⇒ NG // HK và NG = HK : 2
Do D là trung điểm HK
⇒ HD = HK : 2
⇒ HD = NG = HK : 2
Do NG // HK
⇒ NG // HD
Do ∠MHK = 90⁰
⇒ ∠NHD = 90⁰
Tứ giác NGDH có:
NG // HD (cmt)
NG = HD (cmt)
⇒ NGDH là hình bình hành
Mà ∠NHD = 90⁰ (cmt)
⇒ NGDH là hình chữ nhật







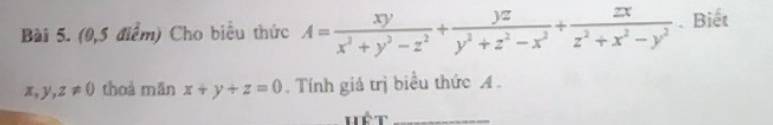

1 leaves
2 speaking
3 famous
4 nationality
5 more
6 different
7 worst
8 thirtieth
9 swimming
10 activities
1.leaves
2.speaking
3.famous
4.nationality
5.more
6.Differ
7.Badly
8.Thirty
9.Swimming
10.Act
Mik ko biết đúng hay ko nha