-2x^2+4x-3m+1=0 Tìm m để phương trình có 2 nghiệm phân biệt thuộc [-5;3]
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\text{Δ}=\left(-4\right)^2-4\cdot2\cdot5\left(m-1\right)\)
\(=16-40\left(m-1\right)\)
\(=16-40m+40\)
=-40m+56
Để phương trình có hai nghiệm phân biệt nhỏ hơn 3 thì
\(\left\{{}\begin{matrix}-40m+56>0\\\dfrac{4}{2}< 6\end{matrix}\right.\Leftrightarrow-40m>-56\)
hay m<7/5
b: Để phương trình có hai nghiệm phân biệt lớn hơn 3 thì
\(\left\{{}\begin{matrix}-40m+56>0\\\dfrac{4}{2}>6\end{matrix}\right.\Leftrightarrow m\in\varnothing\)

Bài 1:
a) Thay m=3 vào (1), ta được:
\(x^2-4x+3=0\)
a=1; b=-4; c=3
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{3}{1}=3\)
Bài 2:
a) Thay m=0 vào (2), ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
hay x=1

Đáp án B



Ta có bảng biến thiên
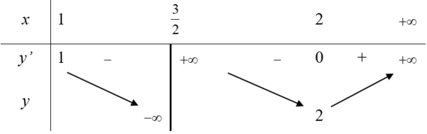
Phương trình (1) có bốn nghiệm phân biệt
⇔ * có hai nghiệm phân biệt lớn hơn 1
Mà m nguyên và m ∈ − 2019 ; 2019 nên ta có m ∈ 3 ; 4 ; ... ; 2018 .
Vậy có 2016 giá trị m thỏa mãn bài toán.

a: Th1: m=0
=>-2x-1=0
=>x=-1/2
=>NHận
TH2: m<>0
Δ=(-2)^2-4m(m-1)=-4m^2+4m+4
Để phương trình có nghiệm duy nhất thì -4m^2+4m+4=0
=>\(m=\dfrac{1\pm\sqrt{5}}{2}\)
b: Để PT có hai nghiệm phân biệt thì -4m^2+4m+4>0
=>\(\dfrac{1-\sqrt{5}}{2}< m< \dfrac{1+\sqrt{5}}{2}\)




