cho tam giác abc vuông tại a trên tia đối của bc lấy điểm m, trên tia dối của cb lấy điểm n sao cho bm =cn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 1 2022
Xét ΔBAM và ΔCAN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
DO dó: ΔBAM=ΔCAN
Suy ra: AM=AN
hay ΔAMN cân tại A
Bn tham khảo nhé!
CM
16 tháng 2 2017
ΔABC cân tại A suy ra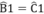 
Ta lại có :
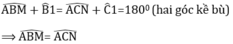
- ΔABM và ΔACN có
AB = AC (Do ΔABC cân tại A).
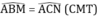
BM = CN(gt)
⇒ ΔABM = ΔACN (c.g.c)
⇒ AM = AN (hai cạnh tương ứng) ⇒ ΔAMN cân tại A.
CM
3 tháng 6 2019
Theo câu b ta có ΔBHM = ΔCKN ⇒ HM = KN (hai cạnh tương ứng)
Mà AM = AN ⇒ AM –MH = AK – KN hay AH = AK.
HL
27 tháng 2 2015
Từ đỉnh A kẻ đường cao AH (H thuộc BC) (1)
Ta có : tam giác ABC cân tại A (gt) (2)
Từ(1) và(2)=> HB=HC(=1/2 BC) (3)
Lại có: BM=CN (gt) (4)
M nằm trên tia đối của tia BC, N nằm trên tia đối của tia CB => M,B,C.N thẳng hàng (5)
Từ (3)và (4)=>HB+BM=HC+CN (6)
Từ (5) và (6)=>AH vừa là đường cao, vừa là đường trung tuyến trong tam giác AMN
=> Tam giác AMN cân tại A (đpcm)
6 tháng 3 2021
Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC(ΔABC cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
BD=CE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
Suy ra: AD=AE(hai cạnh tương ứng)
Ta có: ΔABD=ΔACE(cmt)
nên \(\widehat{DAB}=\widehat{EAC}\)(hai góc tương ứng)
mà \(\widehat{MAB}=\widehat{NAC}\)
Xét ΔAMB vuông tại M và ΔANC vuông tại N có
AB=AC(ΔBAC cân tại A)
\(\widehat{MAB}=\widehat{NAC}\)(cmt)
Do đó: ΔAMB=ΔANC(cạnh huyền-góc nhọn)
Suy ra: AM=AN(hai cạnh tương ứng)
Xét ΔAMN có AM=AN(cmt)
nên ΔAMN cân tại A(Định nghĩa tam giác cân)
Ta có: ΔAMN cân tại A(cmt)
nên \(\widehat{AMN}=\dfrac{180^0-\widehat{MAN}}{2}\)(Số đo của một góc ở đáy trong ΔAMN cân tại A)
hay \(\widehat{AMN}=\dfrac{180^0-\widehat{DAE}}{2}\)(1)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
Ta có: ΔADE cân tại A(cmt)
nên \(\widehat{ADE}=\dfrac{180^0-\widehat{DAE}}{2}\)(Số đo của một góc ở đáy trong ΔADE cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AMN}=\widehat{ADE}\)
mà \(\widehat{AMN}\) và \(\widehat{ADE}\) là hai góc ở vị trí đồng vị
nên MN//DE(Dấu hiệu nhận biết hai đường thẳng song song)
hay MN//BC(đpcm)
CM
14 tháng 9 2017
Khi góc BAC = 60º và BM = CN = BC
Tam giác cân ABC có góc BAC = 60º nên là tam giác đều
⇒ AB = BC và góc B1 = 60º
Ta có: AB = CB, BC = BM (gt) ⇒ AB = BM ⇒ ΔABM cân ở B ⇒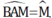 
Mà theo tính chất góc ngoài trong ΔBAM thì
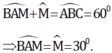
Tương tự ta có
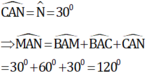
* Ta chứng minh tam giác OBC là tam giác đều.
4 tháng 3 2018
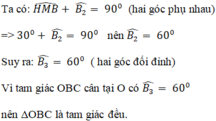
a) Tam giác ABC cân nên hai góc đáy bằng nhau : Góc ACB = Góc ABC
Ta lại có : Góc ABM = 180° - Góc ABC , Góc ACN = 180° - Góc ACB
Vậy Góc ABM = Góc ACN
Xét hai tam giác ABM và CAN , ta có :
AB = AC (gt)
Góc ABM = Góc ACN (cmt)
BM = CN (gt)
=> Tam giác ABM = tam giác CAN => AM = AN
Vậy tam giác AMN là tam giác cân tại A
b) Vì tam giác AMN cân => Góc AMB = Góc ANC
Xét tam giác MHB và tam giác CKN
Ta có : Góc MHB = Góc CKN ( Góc vuông )
Góc AMB = Góc ANC (cmt)
MB = CN (cmt)
=> tam giác MHB = tam giác NKC (g-c-g)
=> BH = CK
c) làm tương tự câu b
d) Tam giác ABM = Tam giác CKN => Góc HBM = Góc KCN
Góc CBO = Góc HBM và Góc KCN = Góc BCO ( đối đỉnh )
=> OBC là tam giác cân tại O
e) Khi BAC = 60° => Tam giác ABC đều
ta suy ra BM = AB => Tam giác ABM cân đỉnh B . Ta có Góc AMB = \(\frac{1}{2}\) ABC = \(\frac{1}{2}\) . 60 = 30°
Làm tương tự cho góc kia thì ANM = 30°
Góc  = 180 - 30° - 30° = 120°
Góc KCN = Góc BCO =60°
bn tham khảo!
bn thiếu đề bài :
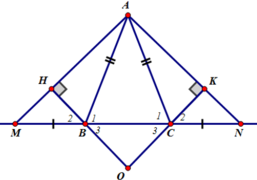
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN
a) Chứng minh rằng tam giác AMN là tam giác cân
b) Kẻ BH vuông góc với AM ( H thuộc AM ). Kẻ CK vuông góc với AN ( K thuộc AN ). Chứng minh rằng BH = CK
c) Chứng minh rằng AH = AK
d) Gọi O là giao điểm của BH và CK. Tam giác OBC là tam giác gì? Vì sao?
e) Khi góc BAC = 60 độ và BM = CN = BC, hãy tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC.