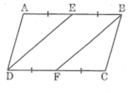
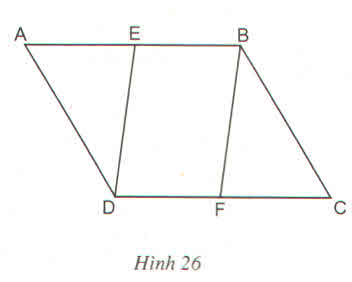
cho hình bình hành abcd gọi 3 là trung điểm của ab,F là trung điểm của CD. chứng minh tam giác ADE song song với tam giác CBF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 3 2017
Vì ABCD là hình bình hành nên:
AB = CD (1)
Theo giả thiết:
AE = EB = 1/2 AB (2)
DF = FC = 1/2 CD (3)
Từ (1), (2) và (3) suy ra:
EB = DF và BE // DF.
Suy ra tứ giác BEDF là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)
Suy ra: DE // BF
Ta có: ∠ (AED) = ∠ (ABF ) (đồng vị)
∠ (ABF) = ∠ (BFC) (so le trong)
Suy ra: ∠ (AED) = ∠ ( BFC)
Xét △ AED'và △ CFB ta có:
∠ (AED) = ∠ ( BFC) (chứng minh trên)
∠ A = ∠ C (tính chất hình bình hành)
Vậy: △ AED đồng dạng △ CFB (g.g)
2 tháng 3 2020
Bài 1:
a) Xét tam giác ABC có M là trung điểm của AB (gt) ,E là trung điểm của AC (gt)
\(\Rightarrow ME\)là đường trung bình tam giác ABC
\(\Rightarrow ME=\frac{1}{2}BC\left(tc\right)\left(1\right)\)
Xét tam giác ADC có E là trung điểm của AC (gt) ,P là trung điểm của DC (gt)
\(\Rightarrow PE\)là đường trung bình của tam giác ADC
\(\Rightarrow PE=\frac{1}{2}AD\left(tc\right)\left(2\right)\)
mà \(AD=BC\left(gt\right)\left(3\right)\)
Từ (1) , (2) và (3) \(\Rightarrow EM=PE\)
CMTT: \(PE=FP,FM=ME\)
\(\Rightarrow ME=EP=PF=FM\)
Xét tứ giác MEPF có:
\(ME=EP=PF=FM\left(cmt\right)\)
\(\Rightarrow MEPF\)là hình thoi ( dhnb)
b) Vì \(MEPF\)là hình thoi (cmt)
\(\Rightarrow FE\)giao với MP tại trung điểm mỗi đường (tc) (4)
Xét tam giác ADB có M là trung điểm của AB(gt) ,Q là trung điểm của AD (gt)
\(\Rightarrow MQ\)là đường trung bình của tam giác ADB
\(\Rightarrow MQ//DB,MQ=\frac{1}{2}DB\left(tc\right)\left(5\right)\)
Xét tam giác BDC có N là trung điểm của BC(gt) , P là trung điểm của DC(gt)
\(\Rightarrow NP\)là đường trung bình của tam giác BDC
\(\Rightarrow NP//DB,NP=\frac{1}{2}DB\left(tc\right)\left(6\right)\)
Từ (5) và (6) \(\Rightarrow MQ//PN,MQ=PN\)
Xét tứ giác MQPN có \(\Rightarrow MQ//PN,MQ=PN\)
\(\Rightarrow MQPN\)là hình bình hành (dhnb)
\(\Rightarrow MP\)giao QN tại trung điểm mỗi đường (tc) (7)
Từ (4) và (7) \(\Rightarrow MP,NQ,EF\)cắt nhau tại một điểm
c) Xét tam giác ABD có Q là trung điểm của AD (gt), F là trung điểm của BD(gt)
\(\Rightarrow QF\)là đường trung bình của tam giác ADB
\(\Rightarrow QF//AB\left(8\right)\)
CMTT: \(FN//CD\)và \(EN//AB\)
Mà Q,F,E,N thẳng hàng
\(\Rightarrow AB//CD\)
Vậy để Q,F,E,N thẳng hàng thì tứ giác ABCD phải thêm điều kiện \(AB//CD\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
12 tháng 9 2023
a/
FB=FC (gt); FD=FG (gt) => BDCG là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
b/
Ax//BC => AH//FB
Fy//AB => FH//AB
=> ABFH là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
=> AH=FB (cạnh đối hbh); Mà FB=FC => AH=FC
Ta có Ax//BC => AH//FC
=> AFCH là hbh (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)
=> AF//HC (cạnh đối hbh)
c/
DA=DB (gt)
FB=FC (gt)
=> J là trọng tâm của tg ABC \(\Rightarrow AJ=\dfrac{2}{3}AF\)
\(HK=\dfrac{1}{3}HC\Rightarrow CK=\dfrac{2}{3}HC\)
Ta có AFCH là hbh (cmt) =>AF=HC
=> AJ=CK (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)
Ta có
AF//HC (cmt) => AJ//CK
=>AKCJ là hbh
Nối J với K cắt AC tại I'
=> I'A=I'C (trông hbh hai đường chéo cắt nhau tại trung điểm mỗi đường) => I' là trung điểm AC
Mà I cũng là trung điểm AC
\(\Rightarrow I'\equiv I\) => J; I; K thẳng hàng