giải phương trình (x^2-3x+3)*(x^2-2x+3)=2x^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) Ta có: \(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
Vậy: S={2}

\(2x^2-6x-3=0\)
\(\Delta'=3^2+3.2=15>0\)
⇒ Phương trình có hai nghiệm phân biệt.
Theo hệ thức viét có : \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=-\dfrac{3}{2}\end{matrix}\right.\)
Ta có : \(A=x_1^2x_2^2-2x_1-2x_2=\left(x_1x_2\right)^2-2\left(x_1+x_2\right)=\left(-\dfrac{3}{2}\right)^2-2.3=-\dfrac{15}{4}\)
Vậy \(A=-\dfrac{15}{4}\) thì thỏa mãn điều kiện bài ra.

a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0
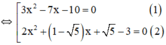
+ Giải (1):
3 x 2 – 7 x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .
+ Giải (2):
2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
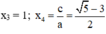
Vậy phương trình có tập nghiệm 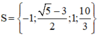
b)
x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0
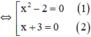
+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c)
x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0
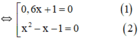
+ Giải (1): 0,6x + 1 = 0 ⇔ 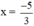
+ Giải (2):
x 2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0
⇒ (2) có hai nghiệm 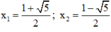
Vậy phương trình có tập nghiệm 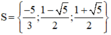
d)
x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0
⇔ (3x-10).x.(2x+1)=0
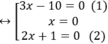
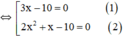
+ Giải (1): 3x – 10 = 0 ⇔ 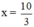
+ Giải (2):
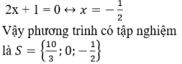

\(\Leftrightarrow\left(x^2-3x+3\right)\left(x^2-3x+3+x\right)-2x^2=0\)
\(\Leftrightarrow\left(x^2-3x+3\right)^2+x\left(x^2-3x+3\right)-2x^2=0\)
\(\Leftrightarrow\left(x^2-3x+3\right)^2-x\left(x^2-3x+3\right)+2x\left(x^2-3x+3\right)-2x^2=0\)
\(\Leftrightarrow\left(x^2-3x+3\right)\left(x^2-3x+3-x\right)+2x\left(x^2-3x+3-x\right)=0\)
\(\Leftrightarrow\left(x^2-4x+3\right)\left(x^2-x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-4x+3=0\\x^2-x+3=0\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)


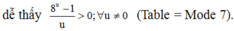
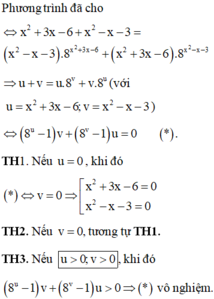

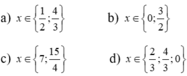
Đặt t=x^2-2x+3 tự giải típ