K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
18 tháng 7 2021
Gọi số sản phẩm àm 2 ng công nhân được giao là x (x∈N*, sản phẩm)
Thời gian hoàn thành công việc của người thứ nhất là: \(\dfrac{x}{40}\left(h\right)\)
Thời gian hoàn thành công việc của ngươi thứ hai là: \(\dfrac{x}{50}\left(h\right)\)
Vì ng thứ nhất hoàn thành công việc chậm hơn người thứ hai 2 giờ nên ta có PT:
\(\dfrac{x}{40}-\dfrac{x}{50}=2\)
⇔\(50x-40x=4000\)
⇔\(10x=4000\)
⇔\(x=400\)
Vậy số sản phẩm mỗi công nhân được giao là 400 (sản phẩm)
TN
Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(
1
5 tháng 8 2021
Bài 3:
2) Ta có: \(B=2x\left(y-z\right)+\left(z-y\right)\left(x+t\right)\)
\(=2x\left(y-z\right)-\left(x+t\right)\left(y-z\right)\)
\(=\left(y-z\right)\left(x-t\right)\)
\(=\left(24-10,6\right)\left(18,3+31,7\right)\)
\(=13,4\cdot50=670\)
3) Ta có: \(C=\left(x-y\right)\left(y+z\right)+y\left(y-x\right)\)
\(=\left(x-y\right)\left(y+z\right)-y\left(x-y\right)\)
\(=z\left(x-y\right)\)
\(=1.5\left(0.86-0.26\right)\)
\(=0,9\)
MP
1
15 tháng 12 2023
Bài IV:
1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(3\right)\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD tại C
=>AC\(\perp\)DM tại C
Xét ΔADM vuông tại A có AC là đường cao
nên \(MC\cdot MD=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MA^2=MH\cdot MO=MC\cdot MD\)
3: Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{OAM}=90^0\)
\(\widehat{HAI}+\widehat{OIA}=90^0\)(ΔAHI vuông tại H)
mà \(\widehat{OAI}=\widehat{OIA}\)
nên \(\widehat{MAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAM
Xét ΔAHM có AI là phân giác
nên \(\dfrac{HI}{IM}=\dfrac{AH}{AM}\left(5\right)\)
Xét ΔOHA vuông tại H và ΔOAM vuông tại A có
\(\widehat{HOA}\) chung
Do đó: ΔOHA đồng dạng với ΔOAM
=>\(\dfrac{OH}{OA}=\dfrac{HA}{AM}\)
=>\(\dfrac{OH}{OI}=\dfrac{AH}{AM}\left(6\right)\)
Từ (5) và (6) suy ra \(\dfrac{OH}{OI}=\dfrac{IH}{IM}\)
=>\(HO\cdot IM=IO\cdot IH\)
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
26 tháng 10 2021
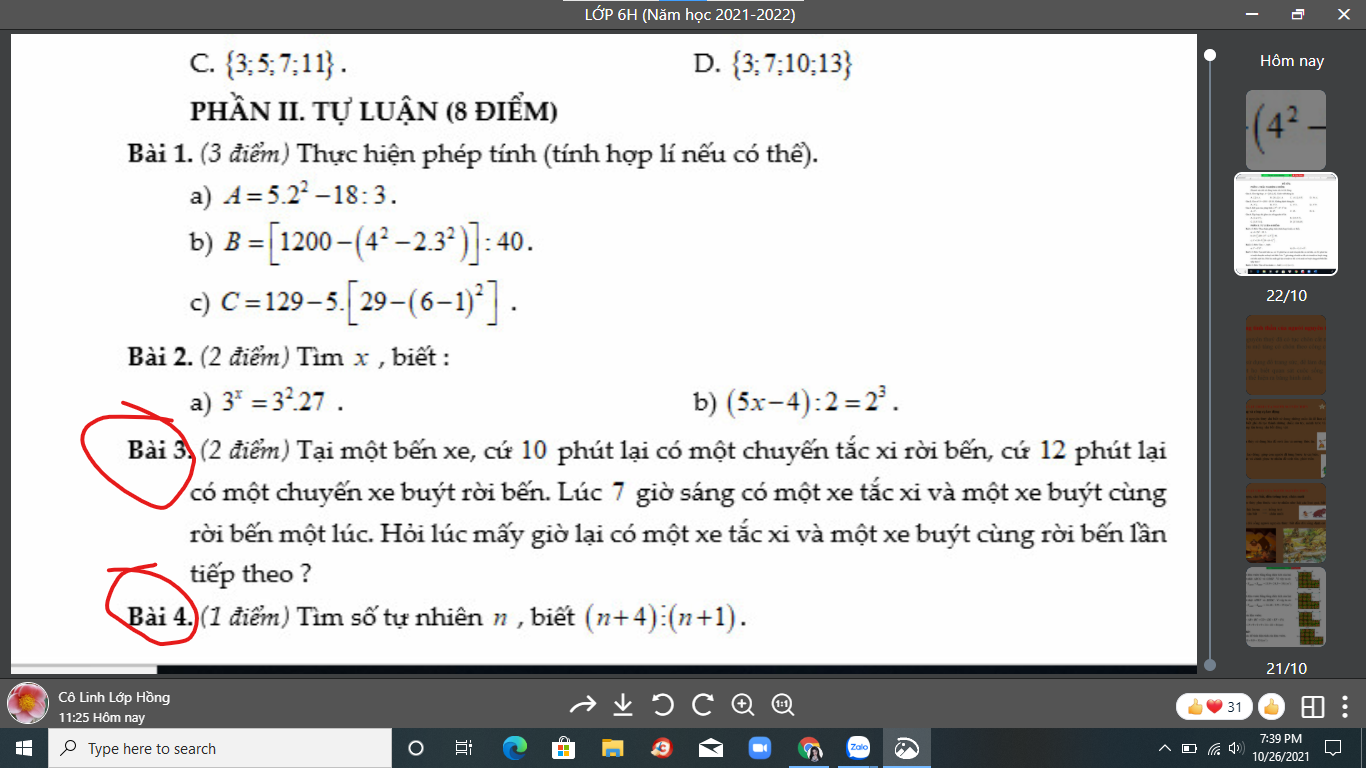
Bài 4:
\(\Leftrightarrow n+1\in\left\{1;3\right\}\)
hay \(n\in\left\{0;2\right\}\)
26 tháng 10 2021
\(\left(n+4\right)⋮\left(n+1\right)\Rightarrow\left(n+1\right)+3⋮\left(n+1\right)\)
\(\Rightarrow\left(n+1\right)\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Mà \(n\in N\)
\(\Rightarrow n\in\left\{0;2\right\}\)
KM
0
AN
2
2 tháng 3 2023
Bài 3.
a. Ta có: \(CK=BK\left(gt\right)\Rightarrow OK\perp BC\)
Ta có: \(\widehat{OIC}=90^o\)
\(\widehat{OKC}=90^o\)
\(\Rightarrow\widehat{OIC}+\widehat{OKC}=90^o+90^o=180^o\)
`=>` Tứ giác CIOK nội tiếp đường tròn
b. Xét \(\Delta AID\) và \(\Delta CIB\), có:
\(\widehat{AID}=\widehat{CIB}=90^o\left(gt\right)\)
\(\widehat{ADI}=\widehat{CBI}\) ( cùng chắn \(\stackrel\frown{AC}\) )
Vậy \(\Delta AID\sim\Delta CIB\) ( g.g)
\(\Rightarrow\dfrac{IA}{IC}=\dfrac{ID}{IB}\)
\(\Leftrightarrow IC.ID=IA.IB\)
c. Kẻ \(DM\perp AC\)
Ta có: \(\widehat{ACB}=90^o\) ( góc nt chắn nửa đtròn )
`->` Tứ giác DMCK là hình chữ nhật
\(\rightarrow DK\perp BC\)
Mà \(OK\perp BC\)
\(\Rightarrow\) 3 điểm D,O,K thẳng hàng
Giúp em bài 3 với ạ. Em cảm ơn ạ
28 tháng 3 2023
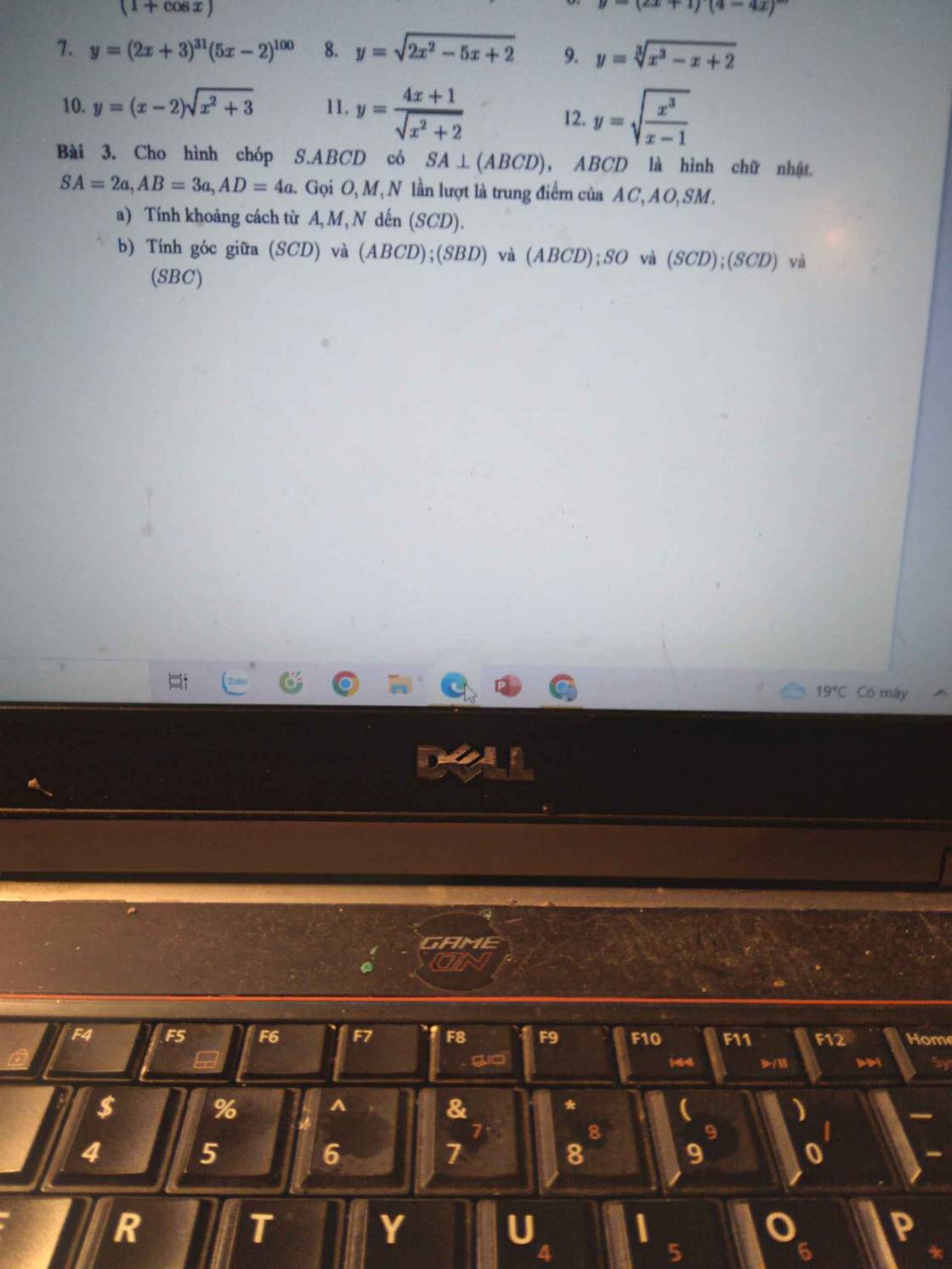
a: AD vuông góc CD
SA vuông góc CD
=>CD vuông góc (SAD)
Kẻ AH vuông góc SD
=>CD vuông góc AH
mà SD vuông góc AH
nên AH vuông góc (CDS)
=>d(A;(SCD))=AH=căn (4a^2+16a^2/8a^2)=căn 10/2
Kẻ MP//AB//CD
=>AP/AD=AM/AC
=>AP/4a=1/4
=>AP=a
=>PD=3a
PQ vuông góc SD
PQ vuông góc CD
=>PQ vuông góc (SCD)
mà PM//(SCD)
nên d(P;(SCD))=PQ
Xét ΔADH có PQ/AH=PD/AD
\(\dfrac{PQ}{\sqrt{10}:2}=\dfrac{3a}{4a}=\dfrac{3}{4}\)
=>PQ=3 căn 10/8
=>d(M;(SCD))=PQ=3căn 10/8
Kẻ NG//AM
Kẻ GU vuông góc SD
=>d(G;(SCD))=GU
GU/AH=SG/SA=1/2
=>GU=căn 10/4
b: (SCD;ABCD))=(AD;SD)=góc ADH
AH=AD*cosADH
=>cosADH=căn 10/8
=>góc ADH=67 độ
(SBD;(ABCD))=góc SOA
SA=AO*tan SOA
=>tan SOA=2/5
=>góc SOA=22 độ