Cho tam giác ABC có góc A =90o .Đg thẳng AH vuông góc vs BC tại H . Trên đg vuông góc vs BC lấy điểm D ko cùng nửa mặt phẳng bờ BC vs điểm A sao cho AH=BD
a, CMR ΔAHB = ΔDBH
b,Hai đg thẳng AB và DH có song song ko ? Vì sao
c, Tính góc ACB biết góc BAH = 35o

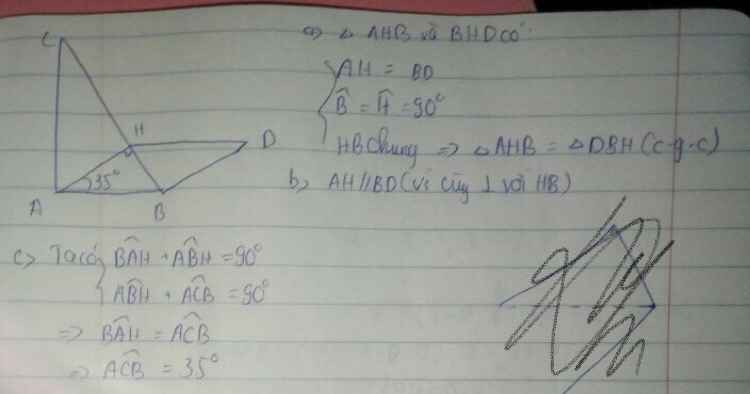
a) Xét ΔAHB vuông tại H và ΔDBH vuông tại B có
HB chung
AH=DB(gt)
Do đó: ΔAHB=ΔDBH(hai cạnh góc vuông)
b) Ta có: ΔAHB=ΔDBH(cmt)
nên \(\widehat{ABH}=\widehat{DHB}\)(hai góc tương ứng)
mà \(\widehat{ABH}\) và \(\widehat{DHB}\) là hai góc ở vị trí so le trong
nên AB//HD(Dấu hiệu nhận biết hai đường thẳng song song)
c) Ta có: ΔAHB vuông tại H(AH\(\perp\)BC)
nên \(\widehat{BAH}+\widehat{ABH}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ABC}=90^0-35^0=55^0\)
Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{C}=90^0-55^0\)
hay \(\widehat{ABC}=35^0\)
Vậy: \(\widehat{ABC}=35^0\)
a) Xét tam giác AHB và tam giác DBH có:
AH=BD (giả thiết)
Góc AHB=góc DBH (=90o)
BH là cạnh chung
=> Tam giác AHB = tam giác DBH (c.g.c)
b) Theo chứng minh phần a: Tam giác AHB = tam giác DBH => Góc ABH = góc BHD (2 góc tương ứng)
Mà góc ABH và góc BHD là 2 góc so le trong => AB//DH
c) Tam giác ABH có: ˆBAH+ˆAHB+ˆABH=180oBAH^+AHB^+ABH^=180o (tổng 3 góc trong tam giác)
=>35o+90o+ˆABH=180o⇒ˆABH=180o−35o−90o=55o35o+90o+ABH^=180o⇒ABH^=180o−35o−90o=55o
Tam giác ABC có: ˆBAC+ˆACB+ˆABC=180oBAC^+ACB^+ABC^=180o(tổng 3 góc trong tam giác)
=>90o+ˆACB+55o=180