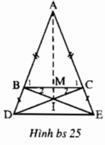
Bài 1. Cho ΔABC cân tại A. Trên tia đối của các tia BA và CA lấy hai điểm D và E sao cho BD = CE.
a) Chứng minh: DE // BC.
b) Chứng minh: BE = CD.
c) BE và CD cắt nhau tại K. Chứng minh: ΔKBC và ΔKDE cân.
d) Chứng minh: AK là tia phân giác của góc BAC.
e) Từ D, E kẻ DM, EN ⊥ BC. Chứng minh: DM = EN.
f) Chứng minh: ΔAMN cân.
Bài 2. Cho ΔABC có góc A nhọn. Kẻ tia Ax ⊥ AB (tia AC nằm giữa Ax và AB ). Kẻ tia Ay ⊥ AC (tia AB nằm giữa Ay và AC). Lấy điểm E và F lần lượt thuộc tia Ax và Ay sao cho AE = AB và AC = AF
a) Chứng minh: BF = CE.
b) Gọi M và N lần lượt là trung điểm của BF và CE. Chứng minh: ΔAMN vuông cân.
Bài 3. Trên cạnh BC của ΔABC lấy 2 điểm E và F sao cho BE = CF. Qua E và F vẽ các đường thẳng song song với BA chúng cắt cạnh AC tại G và H. Qua E vẽ đường thẳng song song với AC cắt AB tại D.
a) Chứng minh: AD = GE.
b) Chứng minh: ΔBDE = ΔFHC.
c) Chứng minh: AB = GE + FH.
Bài 4. Cho tam giác ABC vuông tại A và AB = 2AC. Gọi E là trung điểm của AB. Trên tia đối của tia AC lấy điểm D sao cho AB = AD. Chứng minh rằng: BC ⊥ DE.
Bài 5. Cho tam giác ABC vuông cân tại A, M là trung điểm cạnh BC, E là điểm nằm giữa M và C. Vẽ BH ⊥ AE tại H và CK ⊥ AE tại K. CMR:
a) BH = AK
b) ΔMBH = ΔMAK
c) ΔMHK vuông cân.

Bài 1:
a) Ta có: AB+BD=AD(B nằm giữa A và D)
AC+CE=AE(C nằm giữa A và E)
mà AB=AC(ΔABC cân tại A)
và BD=CE(gt)
nên AD=AE
Xét ΔADE có AD=AE(gt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
⇒\(\widehat{ADE}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔADE cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{ABC}=\widehat{ADE}\)
mà \(\widehat{ABC}\) và \(\widehat{ADE}\) là hai góc ở vị trí đồng vị
nên BC//DE(Dấu hiệu nhận biết hai đường thẳng song song)
b) Ta có: \(\widehat{ABC}+\widehat{DBC}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ECB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{DBC}=\widehat{ECB}\)
Xét ΔDBC và ΔECB có
DB=EC(gt)
\(\widehat{DBC}=\widehat{ECB}\)(cmt)
BC chung
Do đó: ΔDBC=ΔECB(c-g-c)
Suy ra: DC=EB(hai cạnh tương ứng)
c) Ta có: ΔDBC=ΔECB(cmt)
nên \(\widehat{DCB}=\widehat{EBC}\)(hai góc tương ứng)
hay \(\widehat{KBC}=\widehat{KCB}\)
Xét ΔKBC có \(\widehat{KBC}=\widehat{KCB}\)(cmt)
nên ΔKBC cân tại K(Định lí đảo của tam giác cân)
⇒KB=KC(Hai cạnh bên)
Ta có: KB+KE=BE(K nằm giữa B và E)
KC+KD=CD(K nằm giữa C và D)
mà KB=KC(cmt)
và BE=CD(cmt)
nên KE=KD
Xét ΔKED có KE=KD(cmt)
nên ΔKED cân tại K(Định nghĩa tam giác cân)
d) Xét ΔBAK và ΔCAK có
BA=CA(ΔABC cân tại A)
AK chung
BK=CK(cmt)
Do đó: ΔBAK=ΔCAK(c-c-c)
Suy ra: \(\widehat{BAK}=\widehat{CAK}\)(hai góc tương ứng)
mà tia AK nằm giữa hai tia AB,AC
nên AK là tia phân giác của \(\widehat{BAC}\)(đpcm)
e) Ta có: \(\widehat{ABC}=\widehat{ACB}\)(Hai góc ở đáy của ΔABC cân tại A)
mà \(\widehat{ABC}=\widehat{DBM}\)(hai góc đối đỉnh)
và \(\widehat{ACB}=\widehat{ECN}\)(hai góc đối đỉnh)
nên \(\widehat{DBM}=\widehat{ECN}\)
Xét ΔDBM vuông tại M và ΔECN vuông tại N có
BD=CE(gt)
\(\widehat{DBM}=\widehat{ECN}\)(cmt)
Do đó: ΔDBM=ΔECN(cạnh huyền-góc nhọn)
Suy ra: DM=EN(hai cạnh tương ứng)
f) Ta có: ΔDBM=ΔECN(cmt)
nên BM=CN(hai cạnh tương ứng)
Ta có: \(\widehat{ABC}+\widehat{ABM}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC(ΔABC cân tại A)
\(\widehat{ABM}=\widehat{ACN}\)(cmt)
BM=CN(cmt)
Do đó: ΔABM=ΔACN(c-g-c)
Suy ra: AM=AN(hai cạnh tương ứng)
Xét ΔAMN có AM=AN(cmt)
nên ΔAMN cân tại A(Định nghĩa tam giác cân)