Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


BC và AK cắt BC tại H.Ta có HB=HC (AK là trung trực của BC)
=>HC=BC/2.
AH=√(AC²-CH²);
∆ACH~∆COH (tam giác vuông chung góc nhọn tại O)
=>AH/AC=HC/CO=>CO=AC.HC/AH.
=20.12/√(20²-12²)=20.12/16=15.
Gọi AH, BK là hai đường cao, có AH = 10; BK = 12
thấy hai tgiác CAH và CBK đồng dạng => CA/AH = CB/BK
=> CA/10= 2CH/12 => CA = 2,6.CH (1)
mặt khác áp dụng pitago cho tgiac vuông HAC:
CA² = CH² + AH² (2)
thay (1) vào (2): 2,6².CH² = CH² + 102
=> (2,6² - 1)CH² = 102=> CH = 10 /2,4 = 6,5
=> BC = 2CH = 13 cm

ta có:
AH.BC = BK.AC
10.BC = 12.AC
=>BC= 6.AC/5 => BC^2=36.AC^2/25
mặt khác:
AC^2 = AH^2 + BC^2/4 = AH^2 + 36.AC^2/100
=>(1-36/100). AC^2= AH^2 = 100
=> AC^2 = 100^2/8^2
=> AC = 100/8 = 25/2
=> BC = 6.25/2.5=15
tam giac ACH đồng dạng tam giác BKC nên CA/AH = CB/BK
Ai có thể giúp mình với!!!!!!!!!!!!!!!? | Yahoo Hỏi & Đáp
tự thế số vô

AB = 12cm mà AB = AC ( ABC cân tại A )
=> AC = 12 cm.
Xét tam giác vuông ABH và tam giác vuông ACH , ta có:
AB = AC (gt)
B = C ( Tính chất tam giác cân)
=> tam giác ABH = tam giác ACH (hệ quả: cạnh huyền góc nhọn )
=> BH = HC ( Hai cạnh tương ứng của 2 tam giác = nhau )
Mà BH + HC = 10 (cm)
=> BH = HC = 10 : 2 = 5 cm
Theo định lý Py-ta-go, AH2 = AC2-BC2
= 122-52
= 144 - 25
= 119 .

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath

Theo giả thiết AB=AC, BC,AH,AB lập thành cấp số nhân nên ta có hệ:
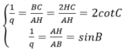
Từ đó ta có kết quả sau: 2cotC = sinC ⇔ 2cosC =sin2C = 1-cos2C
⇔ cos2C + 2cosC -1 =0 ⇒cosC = -1 +√2 (0° < C < 90°)
Do C là góc nhọn nên :
![]()
Cho nên công bội của cấp số nhân là:
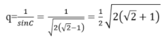
Đáp án C.
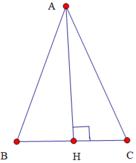

Vì \(\Delta ABC\) cân tại A \(\Rightarrow AH\) là đường cao đồng thời là đường trung tuyến của BC \(\Rightarrow HB=HC=\dfrac{1}{2}BC=\dfrac{1}{2}\cdot24=12cm\)
Áp dụng định lí Pytago vào \(\Delta AHB\) vuông tại H có :
\(HB^2+AH^2=AB^2\) \(\Rightarrow AH^2=AB^2-HB^2=37^2-12^2=1369-144=1225=35^2\Rightarrow AH=35cm\)
Ta có: ΔABC cân tại A(gt)
mà AH là đường cao ứng với cạnh đáy BC(Gt)
nên AH là đường trung tuyến ứng với cạnh BC(Định lí tam giác cân)
⇔H là trung điểm của BC
⇔\(HB=\dfrac{BC}{2}=\dfrac{24}{2}=12\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AH^2=AB^2-BH^2=37^2-12^2=1225\)
\(\Leftrightarrow AH=\sqrt{1225}=35\left(cm\right)\)
Vậy: AH=35cm