Bài 4: Cho ∆ABC cân tại A có Â = 1000. Lấy điểm M thuộc AB, N thuộc AC
sao cho: AM = AN. Chứng minh rằng: MN // BC.
Bài 5*: Cho ∆ABC đều. Lấy các điểm D, E, F theo thứ tự thuộc các cạnh AB, BC, AC sao cho: AD = BE = CF. Chứng minh rằng: ∆DEF đều.
Bài 6: Cho ∆ABC cân tại A, điểm M thuộc cạnh BC. Kẻ MD vuông góc với AB (D thuộc AB); ME vuông góc AC (E thuộc AC); BH vuông góc với AC (H thuộc AC) . Chứng minh MD + ME = BH.
Bài 7: Cho ∆ABC vuông tại A. Kẻ Ax vuông góc với BC tại H. Kẻ phân giác của góc BAH cắt BH tại D. Lấy K trên tia CA sao cho CK = CB.
a) Chứng minh ∆ADC cân. b*) Chứng minh BK // AD, DK // AH.
Bài 8: Cho ∆ABC vuông tại A có góc C=30 độ. Lấy điểm M trên cạnh BC sao cho
BM = BA.
a) Chứng minh ∆AMB đều b) Chứng minh AM = 1/2 BC
Mọi người giúp mình với, mình đang cần đáp án gấp ạ! em cảm ơn nhiều ạ!

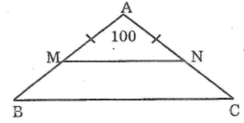

Bài 4 :
- Tam giác ABC cân tại A có :
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow100^o+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=80^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=40^o\left(1\right)\)(tg ABC cân A)
- Xét tg AMN cân tại A (do AM=AN) có : .....(tương tự trên )
\(\Rightarrow\widehat{AMN}=\widehat{ANM}=40^o\left(2\right)\)
- Từ (1) và (2)\(\Rightarrow\widehat{B}=\widehat{AMN}\)
Mà chúng là hai góc đồng vị
=> MN//BC (đccm)
Bài 5:
- Ta có : AD=BE=CF(gt)
=> BD=EC=AF
- Xét tam giác ADF và BED có :
BD=AF(cmt)
AD=BE(gt)
\(\widehat{A}=\widehat{B}\)(tg ABC đều)
=> Tg ADF=BED(c.g.c)
=> DE=DF(1)
- Xét tam giác BED và CFE có :
BE=CF(gt)
BD=CE(cmt)
\(\widehat{B}=\widehat{C}\)(tg ABC đều)
=> Tg BED=CFE(c.g.c)
=> ED=FE(2)
- Từ (1) và (2)=> DE=DF=FE
=> Tg DEF đều