Bài 2. Tính chu vi của tam giác cân ABC, biết:
a) AB = 2cm, AC = 5cm
b) AB = 16cm, AC = 8cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A)vì tam giác ABC là tam giác cân
AB=BC=8
chu vi tam giác ABC=AB+AC+BC=8+5+8=21
B)vì tam giác ABC là tam giác cân
AB=BC=25
chu vi tam giác ABC=AB+AC+BC=25+12+25=62

a) Trường hợp 1: BC=8cm
Chu vi tam giác ACB là:
C=AB+BC+AC=8+13+8=29(cm)
Trường hợp 2: BC=13cm
Chu vi tam giác ABC là:
C=AB+BC+AC=13+13+8=34(cm)

Theo bất đẳng thức tam giác và hệ quả ta có:
AB - AC < BC < AB + AC
=> 6<BC<10
theo đề bài=> BC=8
=> chu vi hình Tam giác= 18 cm (chọn câu C)

Bài 2:
a: AE=AC-CE=16-13=3(cm)
AD=AB-BD=8-2=6(cm)
Xét ΔAED và ΔABC có
AE/AB=AD/AC
\(\widehat{A}\) chung
Do đó: ΔAED∼ΔABC
b: Ta có: ΔAED∼ΔABC
nên AE/AB=AD/AC
hay AB/AC=AE/AD
Xét ΔABE và ΔACD có
AB/AC=AE/AD
\(\widehat{BAE}\) chung
Do đó: ΔABE∼ΔACD
Suy ra: \(\widehat{ABE}=\widehat{ACD}\)

a: Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AB^2=6^2+2^2=40\)
hay \(AB=2\sqrt{10}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=6^2+6^2=72\)
hay \(AC=6\sqrt{2}\left(cm\right)\)

Trường hợp 1: BC=18cm
=>NHận
=>C=AB+BC+AC=36+8=44(cm)
TRường hợp 2: BC=8cm
=>LOại

Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC
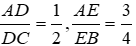

A B C 2 5
a,
+) Chu vi tam giác là : \(2^2+5=9\)cm ( nếu tam giác ABC cân tại B )
+) Chu vi tam giác là : \(5^2+2=27\)cm ( nếu tam giác ABC cân tại C )
b, thay dữ kiện, làm tương tự