Giải phương trình: (x2 - 5x)2 + 10(x2 - 5x) + 24 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1
a/ \(x\left(x^2+1\right)+2\left(x^2+1\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+1\right)=0\Rightarrow x=-2\)
b/
\(\Leftrightarrow x^3-6x^2+9x+5x^2-30x+45=0\)
\(\Leftrightarrow x\left(x-3\right)^2+5\left(x-3\right)^2=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-3\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=3\end{matrix}\right.\)
1.
c/ \(\Leftrightarrow x^3+2x^2+2x+x^2+2x+2=0\)
\(\Leftrightarrow x\left(x^2+2x+2\right)+x^2+2x+2=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+2=0\left(vn\right)\end{matrix}\right.\)
d/
\(\Leftrightarrow x^4+x^3-2x^2-x^3-x^2+2x+4x^2+4x-8=0\)
\(\Leftrightarrow x^2\left(x^2+x-2\right)-x\left(x^2+x-2\right)+4\left(x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x^2-x+4\right)\left(x^2+x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-x+4=0\left(vn\right)\\x^2+x-2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

Bài 1:
a: \(\Leftrightarrow x^2-5x+6< =0\)
=>(x-2)(x-3)<=0
=>2<=x<=3
b: \(\Leftrightarrow\left(x-6\right)^2< =0\)
=>x=6
c: \(\Leftrightarrow x^2-2x+1>=0\)
\(\Leftrightarrow\left(x-1\right)^2>=0\)
hay \(x\in R\)

1) Ta có: \(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
Vậy: S={2}

a: (2x-10)(5x+25)=0
=>2x-10=0 hoặc 5x+25=0
=>x=5 hoặc x=-5
b: (x+15)(x-2)=0
=>x+15=0 hoặc x-2=0
=>x=-15 hoặc x=2
c: =>x(x-7)=0
=>x=0 hoặc x=7

Điều kiện xác định x 2 + 5 x + 10 ≥ 0 ⇔ x ∈ R
Khi đó phương trình ⇔ x 2 + 5 x + 10 + 2 x 2 + 5 x + 10 − 8 = 0
⇔ ( x 2 + 5 x + 10 − 2 ) ( x 2 + 5 x + 10 + 4 ) = 0
⇔ x 2 + 5 x + 10 = 2 x 2 + 5 x + 10 = − 4 ⇔ x 2 + 5 x + 10 = 2 ⇔ x 2 + 5 x + 6 = 0 ⇔ x = − 3 x = − 2
Vậy x 1 2 + x 2 2 = 2 2 + 3 3 = 13
Đáp án cần chọn là: B
giải các Phương trình sau
a) (5x+3)(x2+1)(x-1)=0
b) (4x-1)(x-3)-(x-3)(5x+2)=0
c) (x+6)(3x-1)+x2-36 =0

a: =>(5x+3)(x-1)=0
=>x=1 hoặc x=-3/5
b: =>(x-3)(4x-1-5x-2)=0
=>(x-3)(-x-3)=0
=>x=-3 hoặc x=3
c: =>(x+6)(3x-1+x-6)=0
=>(x+6)(4x-7)=0
=>x=7/4 hoặc x=-6
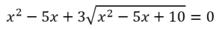
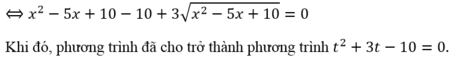
(x2 - 5x)2 + 10(x2 - 5x) + 24 = 0
<=> (x2 - 5x)2 + 10(x2 - 5x) + 25 - 1 = 0
<=> (x2 - 5x + 5)2 - 1 = 0
<=> (x2 - 5x + 4)(x2 - 5x + 6) = 0
<=> (x - 1)(x - 4)(x - 2)(x - 3) = 0
<=> x - 1 = 0 hoặc x - 4 = 0 hoặc x - 2 = 0 hoặc x - 3 = 0
<=> x = 1 hoặc x = 4 hoặc x = 2 hoặc x = 3
Vậy \(x\in\left\{1;2;3;4\right\}\)là nghiệm phương trình
Đặt x2 - 5x = t
pt <=> t2 + 10t + 24 = 0
<=> t2 + 4t + 6t + 24 = 0
<=> t( t + 4 ) + 6( t + 4 ) = 0
<=> ( t + 4 )( t + 6 ) = 0
<=> ( x2 - 5x + 4 )( x2 - 5x + 6 ) = 0
<=> ( x2 - x - 4x + 4 )( x2 - 2x - 3x + 6 ) = 0
<=> [ x( x - 1 ) - 4( x - 1 ) ][ x( x - 2 ) - 3( x - 2 ) ] = 0
<=> ( x - 1 )( x - 2 )( x - 3 )( x - 4 ) = 0
<=> x = 1 hoặc x = 2 hoặc x = 3 hoặc x = 4
Vậy phương trình có tập nghiệm S = { 1 ; 2 ; 3 ; 4 }