cho hình chóp tứ giác SABCD đáy ABCD là hình thang AD//BC, AD = 2a, BC= a, gọi o là giao điểm AC và BD.
Tính cv và Diện tích của thiết diện khi ABCD là hình thang cân và SA=SD=2a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
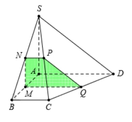
Gọi N, Q lần lượt là trung điểm của AB, CD ⇒ M N ⊥ A B M Q ⊥ A B .
Qua N kẻ đường thẳng song song với BC, cắt SC tại P.
Suy ra thiết diện của mặt phẳng α và hình chóp là MNPQ.
Vì MQ là đường trung bình của hình tháng ABCD ⇒ M Q = 3 a 2 .
MN là đường trung bình của tam giác SAB ⇒ M N = S A 2 = a .
NP là đường trung bình của tam giác SBC ⇒ N P = B C 2 = a 2 .
Vậy diện tích hình thang MNPQ là S M N P Q = M N . N P + M Q 2 = a 2 a 2 + 3 a 2 = a 2 .

Vì SA vuông góc (ABCD)
=>SA vuông góc CD
Gọi I là trung điểm của AD
=>AI=BC=a
mà AI//BC
nên AB=CI=a
=>AB=CI=ID
=>ΔACD vuông tại C
=>CD vuông góc AC
=>CD vuông góc (SAC)
=>(SCD) vuông góc (SAC)
Vẽ AE vuông góc SC tạiE
=>AE vuông góc (SCD)
mà \(A\in\left(P\right)\perp\left(SCD\right)\)
nên \(AE\in\left(P\right)\)
=>\(E=SC\cap\left(P\right)\)
\(E\in\left(P\right)\cap\left(SCI\right)\)
\(\left(P\right)\supset AB\)//CI thuộc (SCI)
=>(P) cắt (SCI)=Ex//AB//CI
Gọi F=Ex giao SI
=>(P) cắt (SAD) tại AJ
Gọi F=AJ giao SD
=>F=(P)giao (SD)
=>Tứ giác cần tìm là ABEF

Đáp án A
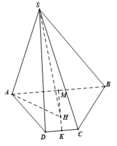
∆ DCM là tam giác đều cạnh a
=> SH ⊥ (ABCD) với H là tâm của ∆ DCM
Do đó (SA;(ABCD)) ![]()

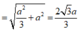
![]()
![]()
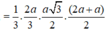
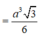

Gọi N, Q lần lượt là trung điểm của AB , CD \(\Rightarrow\left\{{}\begin{matrix}MN\perp AB\\MQ\perp AB\end{matrix}\right.\)
Qua N kẻ đường thẳng song song với BC , cắt SC tại P
suy ra thiết diện của mặt phẳng (\(\alpha\) ) và hình chóp là MNPQ
Vì MQ là đường t/b của hình thang ABCD , \(\Rightarrow MQ=\dfrac{3a}{2}\)
MN là đường t/b của tam giác SAB; \(MN=\dfrac{SA}{2}=a\)
NP là đường t/b của tam giác SBC ; \(\Rightarrow NP=\dfrac{BC}{2}=\dfrac{a}{2}\)
Vậy diện tích hình thang MNPQ là : \(S_{MNPQ}=\dfrac{MN.\left(NP+MQ\right)}{2}=\dfrac{a}{2}.\left(\dfrac{a}{2}+\dfrac{3a}{2}\right)=a^2\)
Bạn xem lại câu hỏi nhé. Thiết diện cắt bởi mặt phẳng nào nhỉ?
minh viết thiếu thiết diện cắt bơi mp (anpha) qua o // SD và BC