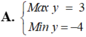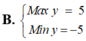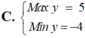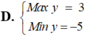Tìm Min của biểu thức F(x;y) = x-2y với điều kiện \(\left\{{}\begin{matrix}0\le y\le5\\x\ge0\\x+y-2\ge0\\x-y-2\le0\end{matrix}\right.\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 1 2021
Con bạn bảo mk chỉ biết là Min F=1 khi x=2 và y=3
23 tháng 12 2017
Với mọi x ta có :
\(A=\left|x-3\right|+\left|x-2\right|\)
\(\Leftrightarrow A=\left|x-3\right|+\left|2-x\right|\)
\(\Leftrightarrow A\ge\left|x-3+2-x\right|\)
\(\Leftrightarrow A\ge\left|-1\right|\)
\(\Leftrightarrow A\ge1\)
Dấu "=" xảy ra khi :
\(\left(x-3\right)\left(2-x\right)\ge0\)
\(\Leftrightarrow\orbr{\begin{cases}\hept{\begin{cases}x-3\ge0\\2-x\ge0\end{cases}}\\\hept{\begin{cases}x-3\le0\\2-x\le0\end{cases}}\end{cases}}\)
NT
0
10 tháng 11 2021
\(1,Sửa:A=4x^4+4x^2y+y^2+2=\left(2x^2+y\right)^2+2\ge2\\ A_{min}=2\Leftrightarrow2x^2+y=0\Leftrightarrow x^2=-\dfrac{y}{2}\\ 2,B=\left(x+y\right)^2+\left(y+1\right)^2+12\ge12\\ B_{min}=12\Leftrightarrow\left\{{}\begin{matrix}x=-y=1\\y=-1\end{matrix}\right.\)
B
3
1 tháng 10 2018
(x−1)(x+2)(x+3)(x+6)= [(x−1)(x+6)][(x+2)(x+3)] = (x^2+5x−6)(x^2+5x+6) = (x^2−5x)^2−36≥−36
=> Giá trị nhỏ nhất biểu thức đã cho là -36 xảy ra khi và chỉ khi (x^2−5x)^2=0
<=> x(x−5)=0
<=> x=0 hoặc x−5=0
<=> x=0 hoặc x=5
1 tháng 10 2018
C=(x+1)(x-2)(x-3)(x-6)
=(x+1)(x-6)(x-2)(x-3)
=(x^2-5x-6)(x^2-5x+6)
=(x^2-5x)^2-6^2
=[x(x-5)]^2-6^2
để Cmin thì [x(x-5)]^2 phải min
mà [x(x-5)]^2\(\ge\)0 nên [x(x-5)]^2min=0 =>C=0-6^2=-6^2
<=>x=0 hoặc x-5=0<=>x=5
vậy Cmin=-6^2 khi x=0 hoặc x=5
