Gọi S(n) là tổng tất cả các chữ số của số nguyên dương n khi biểu diễn nó trong hệ thập phân. Biết rằng với mọi số nguyên dương n thì ta có 0<S(n)<=n. Tìm số nguyên dương n sao cho S(n)=n^2- 2011n+ 2010
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 6 2023
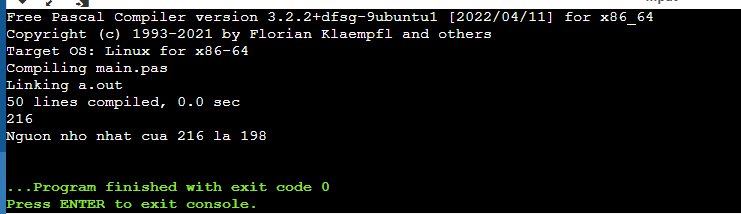
program tim_nguon_nho_nhat;
const
MAX_NUMBER = 10000;
var
M, nguon_nho_nhat: Integer;
function TinhTongChuSo(num: Integer): Integer;
var
sumOfDigits: Integer;
begin
sumOfDigits := 0;
while num > 0 do
begin
sumOfDigits := sumOfDigits + (num mod 10);
num := num div 10;
end;
TinhTongChuSo := sumOfDigits;
end;
function TimNguonNhoNhat(M: Integer): Integer;
var
N, M_temp, M_digits, nguon_nho_nhat: Integer;
begin
M_temp := M;
nguon_nho_nhat := MAX_NUMBER;
for N := 1 to M_temp do
begin
M_digits := TinhTongChuSo(N) + N;
if M_digits = M_temp then
begin
if N < nguon_nho_nhat then
nguon_nho_nhat := N;
end;
end;
if nguon_nho_nhat = MAX_NUMBER then
TimNguonNhoNhat := 0
else
TimNguonNhoNhat := nguon_nho_nhat;
end;
begin
Readln(M);
nguon_nho_nhat := TimNguonNhoNhat(M);
if nguon_nho_nhat = 0 then
Writeln('0')
else
Writeln('Nguon nho nhat cua ', M, ' la ', nguon_nho_nhat);
end.
8 tháng 1 2015
dễ thấy để S(n) và S(n+1) đều chia hết cho 1 số thì đuôi của n kết thúc bằng các số 9.
giả sử n có x số 9 cuối(ta tìm x nhỏ nhất)
khi đó n có dạng a 99...9 (x số 9)
=> n+1=b00...0 ( x+1 số 0) với b=a+1
do S(n) ≡ S(n+1) (mod 7) => a+9x ≡ b (mod 7) => 9x ≡ 1 (mod 7)
=> x=4
=> n=a9999
mà S(n) chia hết cho 7 => a=6 => n=69999 là nhỏ nhất thỏa mãn :D
6 tháng 12 2023
Ta thấy \(87=1.87=3.29\) nên ta xét 2TH
TH1: \(\left\{{}\begin{matrix}S\left(n\right)=1\\S\left(n+1\right)=87\end{matrix}\right.\)
Vì \(S\left(n\right)=1\) nên \(n=100...00\), do đó \(n+1=100...01\) nên \(S\left(n+1\right)=2\), mâu thuẫn.
TH2: \(\left\{{}\begin{matrix}S\left(n\right)=87\\S\left(n+1\right)=1\end{matrix}\right.\)
Vì \(S\left(n+1\right)=1\) nên \(n+1=100...00\), do đó \(n=999...99\) chia hết cho 9, dẫn đến \(S\left(n\right)⋮9\), mâu thuẫn với \(S\left(n\right)=87\)
TH3: \(\left\{{}\begin{matrix}S\left(n\right)=3\\S\left(n+1\right)=29\end{matrix}\right.\)
Vì \(S\left(n\right)=3\) nên \(n⋮3\) \(\Rightarrow n+1\) chia 3 dư 1 \(\Rightarrow S\left(n+1\right)\) chia 3 dư 1. Thế nhưng 29 chia 3 dư 2, vô lý.
TH4: \(\left\{{}\begin{matrix}S\left(n\right)=29\\S\left(n+1\right)=3\end{matrix}\right.\) . Ta lại xét các TH:
TH4.1: \(n+1=10...010...01\) hoặc \(200...01\) hoặc \(100...2\). Khi đó trong tất cả các TH thì ta đều có \(S\left(n\right)=2\), không thỏa mãn.
TH4.2: \(n+1=10...010...010...0\) hoặc \(200...0100...0\) hoặc \(100...020...0\) hoặc \(300...00\). Khi đó trong tất cả các TH thì ta đều có\(S\left(n\right)=2+9m\left(m\inℕ\right)\) với m là số chữ số 9 có trong n. Để chọn được số nhỏ nhất, ta chỉ việc lược bỏ tất cả các số 0 ở giữa và cho \(m=3\) để có \(S\left(n\right)=29\). Vậy, ta tìm được \(n=11999\) (thỏa mãn)
Vậy, số cần tìm là 11999.
11 tháng 5
S(n).S(n+1)=3.29=1.87S(n).S(n+1)=3.29=1.87
- Nếu S(n)=1⇒S(n)=1⇒ nn có dạng 100...0100...0 ⇒S(n+1)=2≠87⇒S(n+1)=2≠87 (loại)
⇒S(n).S(n+1)=3.29⇒S(n).S(n+1)=3.29
Gọi nn có dạng ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯a1a2...aka1a2...ak¯ với ai∈N;a1≠0ai∈N;a1≠0
- Nếu ak≠9⇒S(n+1)=S(n)+1⇒S(n)ak≠9⇒S(n+1)=S(n)+1⇒S(n) và S(n+1)S(n+1) luôn khác tính chẵn lẻ ⇒S(n).S(n+1)⇒S(n).S(n+1) là một số chẵn, mà 87 lẻ ⇒⇒ loại
⇒ak=9⇒ak=9 ⇒S(n)>S(n+1)⇒{S(n)=29S(n+1)=3⇒S(n)>S(n+1)⇒{S(n)=29S(n+1)=3 ⇒S(n)−S(n+1)=26⇒S(n)−S(n+1)=26
Giả sử tận cùng bằng xx số 9 ⇒n=¯¯¯¯¯¯¯¯¯¯¯¯¯¯A9...9⇒n=A9...9¯ với A có tận cùng khác 9
⇒n+1=¯¯¯¯¯¯¯¯¯¯¯¯¯¯B0...0⇒n+1=B0...0¯ (x số 0 và B=A+1B=A+1)
⇒{S(n)=S(A)+9.xS(n+1)=S(B)=S(A+1)=S(A)+1⇒{S(n)=S(A)+9.xS(n+1)=S(B)=S(A+1)=S(A)+1
⇒S(n)−S(n+1)=9x−1=26⇒9x=27⇒x=3⇒S(n)−S(n+1)=9x−1=26⇒9x=27⇒x=3
Vậy n=¯¯¯¯¯¯¯¯¯¯¯¯A999⇒S(n)=S(A)+27=29⇒S(A)=2n=A999¯⇒S(n)=S(A)+27=29⇒S(A)=2
Mà nn nhỏ nhất khi AA nhỏ nhất, ta có số nhỏ nhất có tổng các chữ số bằng 2 là 2 ⇒A=2⇒A=2
⇒n=2999
\(^∗\)Xét \(n=2011\)thì \(S\left(2011\right)=2011^2-2011.2011+2010=2010\)(vô lí)
\(^∗\)Xét \(n>2011\)thì \(n-2011>0\)do đó \(S\left(n\right)=n\left(n-2011\right)+2010>n\left(n-2011\right)>n\)(vô lí do \(S\left(n\right)\le n\))
* Xét \(1\le n\le2010\)thì \(\left(n-1\right)\left(n-2010\right)\le0\Leftrightarrow n^2-2011n+2010\le0\)hay \(S\left(n\right)\le0\)(vô lí do \(S\left(n\right)>0\))
Vậy không tồn tại số nguyên dương n thỏa mãn đề bài