Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a)
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{30^2+40^2}=50$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{30.40}{50}=24$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{30^2-24^2}=18$ (cm)
b)
Theo tính chất tia phân giác:
$\frac{AD}{DC}=\frac{AB}{BC}=\frac{30}{50}=\frac{3}{5}$
$\Rightarrow \frac{AD}{AC}=\frac{3}{8}$
$\Leftrightarrow \frac{AD}{40}=\frac{3}{8}$
$\Rightarrow AD=15$ (cm)
$DC=AC-AD=40-15=25$ (cm)

Ta có: ΔABC cân tại A
mà AD là đường cao
nên D là trung điểm của BC
Xét ΔABC có
D là trung điểm của BC
N là trung điểm của AB
Do đó; DN là đường trung bình
=>DN//AC
tk
https://hoc24.vn/cau-hoi/cho-tam-giac-abc-can-tai-a-co-duong-cao-ah-va-m-la-trung-diem-cua-ab-n-la-trung-diem-cua-ac-goi-d-la-diem-doi-xung-cua-h-qua-m-a-chung-minh-tu-gia.329501118371#:~:text=T%E1%BB%B1%20v%E1%BA%BD%20h%C3%ACnh,r%E1%BB%93i%20T.T

Ta có :
S ABC = 30 X 45 : 2 = 675 cm2
S ABN = 2/3 x 675 = 450 cm2
S AMN = 2/3 X 450 = 300 cm2
Đ/s : 300 cm2
Giúp cháu vs ạ cháu mua 1 hộp kem rick có trọng lượng 454g giá 47k vậy 100g thì bao nhiêu tiền ạ và cho cháu xin công thức tính vs ạ

Áp dụng định lí Pytago vào tam giác vuông ABC ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100
Suy ra: BC = 10cm
Do M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC
Suy ra:
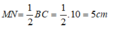
Chọn đáp án C

a) vì M là tđ AB -> AM=1/2AB=5cm
N là tđ AC -> AN=1/2AC= 12cm
áp dụng pytago vào tam giác ANM => MN=13cm
b) theo công thức tính diện tích tam giác ANM (cái này mình chưa biết bạn học chưa, nếu chưa thì nhắn cho mình giải thích cho)
1/2(AM x AN) = 1/2(MN x AH)
=> AM x AN = MN x AH -> 5 x 12 = 13 x AH
=> AH=60/13cm
c) xét 2 tam giác BKM vuông tại K và AHM vuông tại H
có góc AMH + góc BMK ( đối đỉnh )
AM=MB ( M là Tđ AB)
=> 2 tam giác BKM=AHM (cạnh huyền góc nhọn)
d) áp dụng pytago vào tam giác AHM vuông tại H
AM2-AH2=HM2 => HM=MK=25/13cm (vì 2 tam giác ở câu c bằng nhau)
tam giác ABC có góc A vuông
ta có : BC2 = AB2 +AC2 ( định lý pytago )
thay BC2 = 102 + 242
=> BC=26 cm
ta lại có : M là trung điểm của AB => AM=1/2AB=1/2 . 10 =5 cm
tương tự : N là trung điểm của AC => AN = 1/2AC = 1/2 .24 = 12 cm
tam giác AMN vuông tại A , ta có : MN2 = AM2 + AN2 ( định lí pytago )
thay MN2 = 52 + 122
=> MN = 13 cm
Vậy MN = 13 cm

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và \(MN=\dfrac{AC}{2}\)
\(\Leftrightarrow MN=\dfrac{12}{2}=6\left(cm\right)\)
b: Ta có: MN//AC và \(MN=\dfrac{AC}{2}\)
mà P\(\in\)AC và \(AP=\dfrac{AC}{2}\)(P là trung điểm của AC
nên MN//AP và MN=AP
Xét ΔABC có
M là trung điểm của AB
P là trung điểm của AC
Do đó: MP là đường trung bình của ΔABC
Suy ra: MP//BC và \(MP=\dfrac{BC}{2}\)
mà N\(\in\)BC và \(BM=\dfrac{BC}{2}\)
nên MP//BN và MP=BN
Xét tứ giác AMNP có
MN//AP
MN=AP
Do đó: AMNP là hình bình hành
Xét tứ giác BMPN có
MP//BN
MP=BN
Do đó: BMPN là hình bình hành
c) Hình bình hành AMNP trở thành hình vuông khi \(\left\{{}\begin{matrix}\widehat{MAP}=90^0\\AM=AP\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{BAC}=90^0\\AB=AC\end{matrix}\right.\)
Lời giải:
a) Do tam giác $ABC$ vuông tại $A$ nên:
$S_{ABC}=\frac{AB.AC}{2}=\frac{30.40}{2}=600$ (cm2)
b) Do $M,N$ lần lượt là trung điểm của $AB, AC$ nên:
$AM=\frac{1}{2}AB=\frac{1}{2}.30=15$ (cm)
$AN=\frac{1}{2}AC=\frac{1}{2}.40=20$ (cm)
$S_{AMN}=\frac{AM.AN}{2}=\frac{15.20}{2}=150$ (cm2)
$S_{MNCB}=S_{ABC}-S_{AMN}=600-150=450$ (cm2)
Hình vẽ: