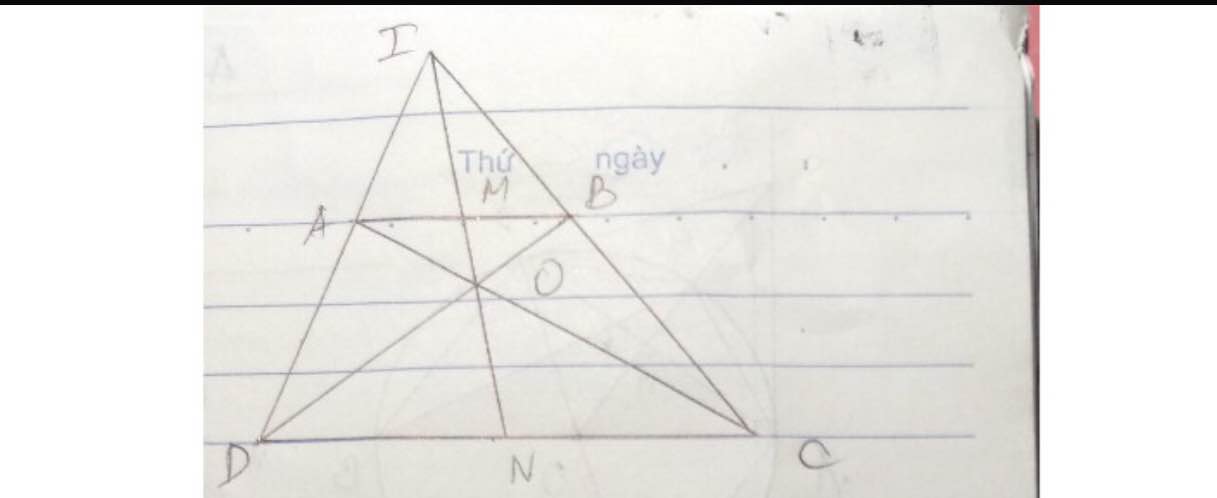
cho hình thang ABCD (AB//CD)M là trung điểm AB ,O là giao của AD và BC, OM cắt CD tại N,CM: N là trung điểm CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
24 tháng 1 2022
- Xét tam giác ODN có: AM//DN.
=>\(\dfrac{AM}{DN}=\dfrac{OM}{ON}\)(định lí Ta-let) (1)
- Xét tam giác OCN có: BM//CN.
=>\(\dfrac{BM}{CN}=\dfrac{OM}{ON}\)(định lí Ta-let) (2)
- Từ (1) và (2) suy ra \(\dfrac{AM}{DN}=\dfrac{BM}{CN}\)mà AM=BM (M là trung điểm AB)
Nên DN=CN. Vậy N là trung điểm của CD.
9 tháng 2 2020
Đây là một định lý trong hình thang , phát biểu rằng:
Trong 1 hình thang có 2 đáy không bằng nhau, trung điểm 2 cạnh đáy, giao điểm 2 đường chéo và giao điểm 2 cạnh bên thẳng hàng.
Chứng minh bài của bạn sẽ sử dụng Định lý TALET như sau
\
Ta có AB // CD (gt)
Áp dụng định lý Ta-let ta được:
\(\frac{AM}{DN}=\frac{OM}{ON};\frac{OM}{ON}=\frac{BM}{CN}\Rightarrow\frac{AM}{DN}=\frac{BM}{CN}\)(hệ quả Talet)
mà AM=BM ( do M là trung điểm AB)
=> DN=NC mà N thuộc DC
=> N là trung điểm DC
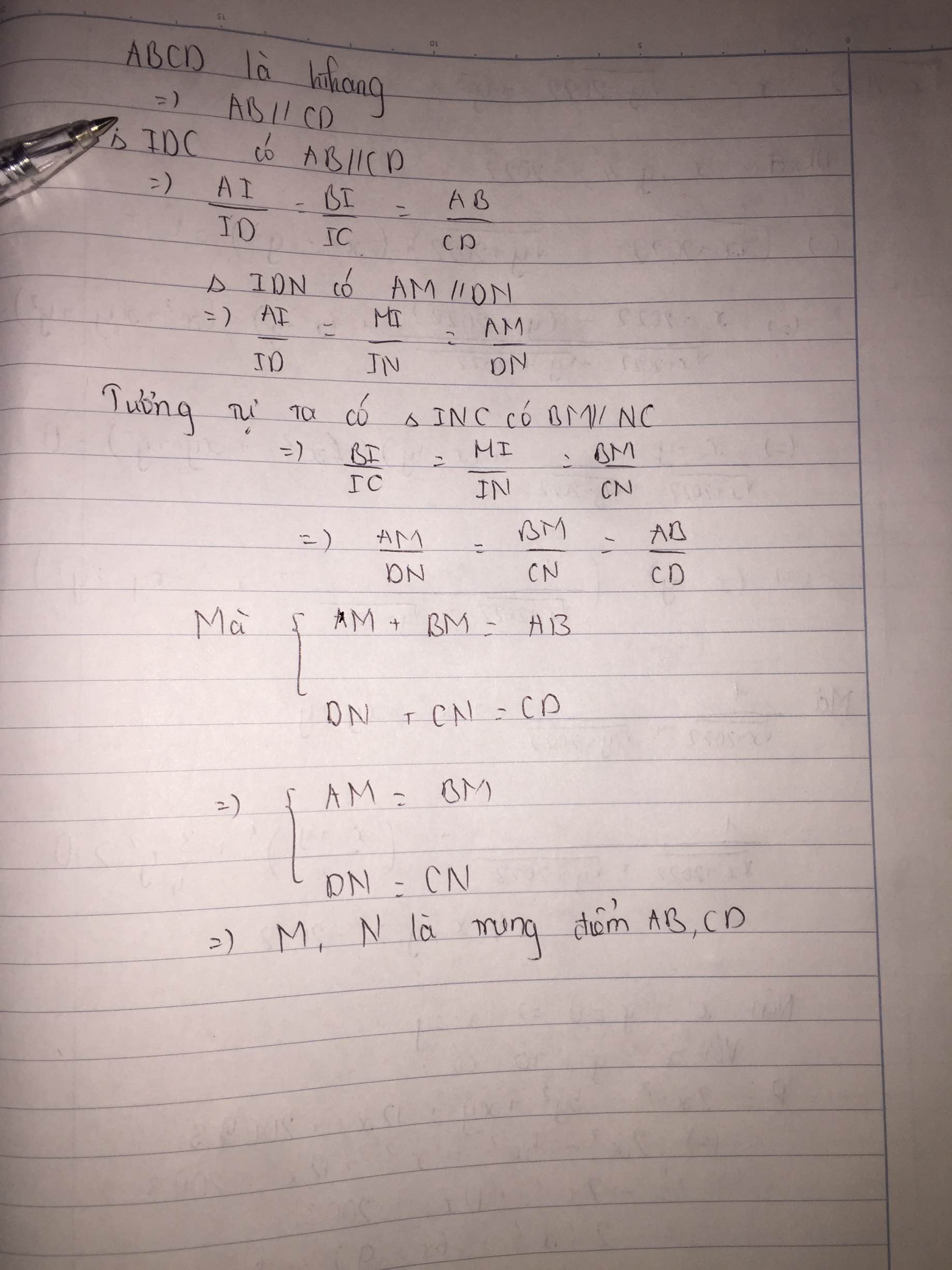
Rồi sao nữa bn?
hết rùi