cho đường tròn (O:C)và dây AB cố dịnh (AB<2R).Từ diêmC bất kì trên tia đối ACB,tiếp tuyến CD với đường tròn(Dthuộc (O)) .Gọi I là trung điêm cua ABTia DIC cắt đường tròn (O) tại điêm thứ 2 K .Kẻ đường thẳng KE SONG SONG với AB.CM
a)CD bình phương =CA.CB
b)tứ giác CDOI nội tiếp
c)CE là tiếp tuyến của đường tròn (O)
d)Khi C chuyển động trên tia đối của AB thì trọng tâm G của tam giác ABD chuyển động trên 1 đường tròn cố định



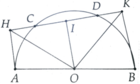
a) Xét \(\Delta CDA\) và \(\Delta CBD\) có:
\(\left\{{}\begin{matrix}\widehat{ACD}-\text{góc chung}\\\widehat{CDA}=\widehat{CBD}\left(=\dfrac{1}{2}\stackrel\frown{AD}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta CDA\sim\Delta CBD\left(g.g\right)\)
\(\Rightarrow\dfrac{CD}{CA}=\dfrac{CB}{CD}\Rightarrow CD^2=CA.CB\).
b) Ta dễ dàng chứng minh được \(\widehat{ODC}=\widehat{OIC}=90^o\), do đó tứ giác CDOI nội tiếp đường tròn đường kính OC.
c) Theo tính chất đối xứng, ta có E, K đối xứng với nhau qua OI.
Do tứ giác CDOI nội tiếp nên \(\widehat{DIO}=\widehat{DCO}\).
Ta biến đổi góc: \(\widehat{COE}=\widehat{IOC}-\widehat{EOI}=\widehat{IOC}-\widehat{KOI}=\widehat{IOC}-\widehat{DIO}+\widehat{OKD}=\widehat{IOC}-\widehat{DIO}+\widehat{ODI}=\widehat{IOD}-\widehat{DOC}-\widehat{DIO}+\widehat{ODI}=180^o-\widehat{DIO}-\widehat{ODI}-\widehat{DOC}-\widehat{DIO}+\widehat{ODI}=180^o-2\widehat{DIO}-\widehat{DOC}=180^o-2\widehat{DCO}-90^o+\widehat{DCO}=90^o-\widehat{DCO}=\widehat{COD}\).
Từ đó \(\Delta DOC=\Delta EOC\left(c.g.c\right)\) nên CE cũng là tiếp tuyến của (O).
d) Do G là trọng tâm của tam giác ABD nên G nằm trên DI và \(DG=\dfrac{2}{3}DI\).
Dựng O' trên cạnh OI sao cho \(OO'=\dfrac{2}{3}OI\).
Theo định lý Thales đảo ta có O'G // OD.
Từ đó \(O'G=\dfrac{1}{3}OD=\dfrac{1}{3}R\) không đổi.
Mà I, O cố định nên O' cố định, từ đó G luôn di chuyển trên đường tròn \(\left(O';\dfrac{1}{3}R\right)\) cố định.
(Đây là một ứng dụng của phép vị tự)