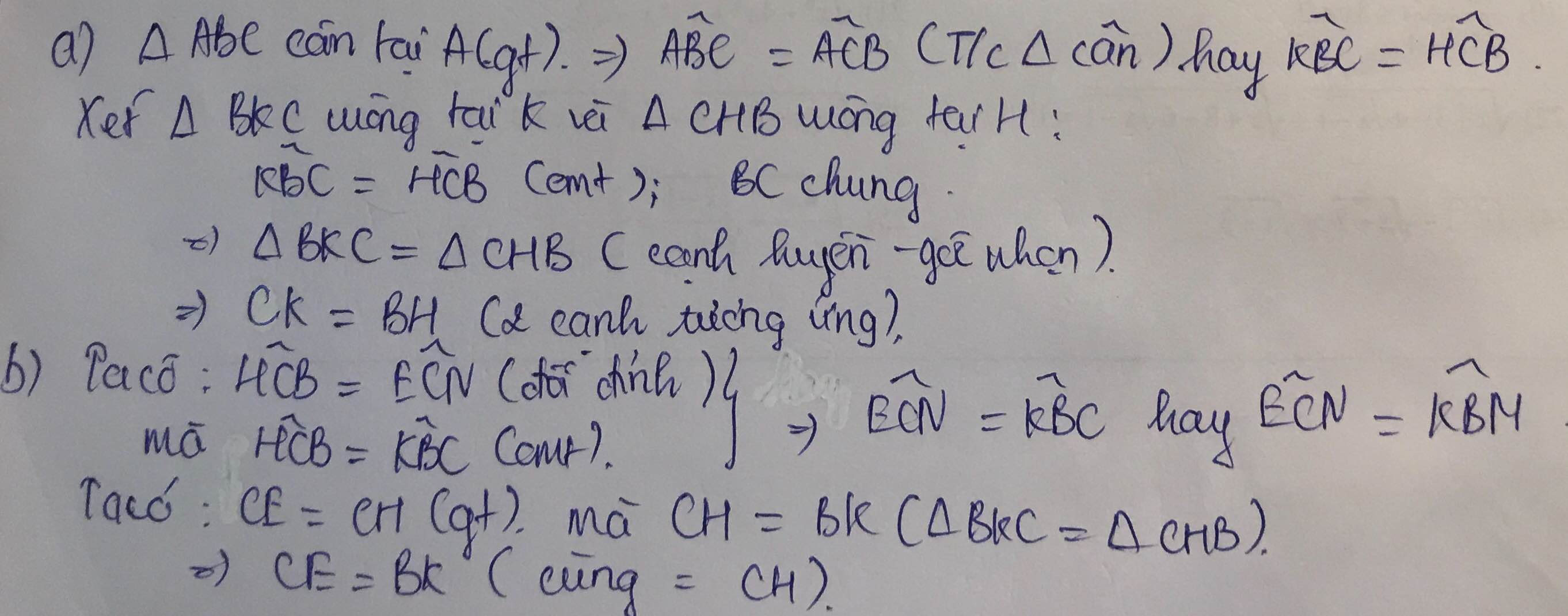cho hình vuông ABCD lấy điểm I trên cạnh BC . Kẻ BH vuông góc với ID ( H thuộc ID ) . Tính góc AHC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A D C B I K P
Ta có \(\widehat{AIP}=\widehat{DAP}\) (Cùng phụ với góc ADI) nên \(\Delta IAP\sim\Delta ADP\left(g-g\right)\)
\(\Rightarrow\frac{AP}{DP}=\frac{AI}{DA}\Rightarrow\frac{AP}{DP}=\frac{AK}{DC}\)
Lại có \(\widehat{IAD}=\widehat{ADP}\) nên \(\widehat{PAK}=\widehat{PDC}\) (Cùng phụ với hai góc trên)
Vậy nên \(\Delta PAK\sim\Delta PDC\left(c-g-c\right)\)
\(\Rightarrow\widehat{APK}=\widehat{DPC}\)
\(\Rightarrow\widehat{APK}+\widehat{KPD}=\widehat{DPC}+\widehat{KPD}\)
\(\Rightarrow\widehat{APD}=\widehat{KPC}\)
\(\Rightarrow\widehat{KPC}=90^o\)
Vậy nên CP vuông góc KP.

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: \(\widehat{D}=\widehat{E}\)
Xét ΔHDB vuông tại H và ΔKEC vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔHDB=ΔKEC
Suy ra: BH=CK
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
Do đó: ΔAHB=ΔAKC

1: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK
Suy ra: BH=CK
2: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó: ΔKBC=ΔHCB
Suy ra:KB=HC
=>KB=CE
Xét ΔKBM vuông tại M và ΔECN vuông tại N có
KB=EC
\(\widehat{KBM}=\widehat{ECN}\left(=\widehat{ACB}\right)\)
Do đó: ΔKBM=ΔECN
Suy ra: KM=EN
Xét tứ giác KMEN có
KM//EN
KM=EN
Do đó: KMEN là hình bình hành
Suy ra: Hai đường chéo KE và MN cắt nhau tại trung điểm của mỗi đường
hay I là trung điểm của KE

a: Xét ΔDHB vuông tại H và ΔEKC vuông tại K có
BD=CE
góc DBH=góc ECK
=>ΔDHB=ΔEKC
=>BH=CK
b: Tham khảo: