Cho hai đường tròn (O) và (O’) cắt nhau ở A và B, O nằm trên đường tròn (O'). Dây AC của (O) cắt (O') ở D, dây OE của (O') cắt (O) ở F. Chứng minh rằng:
a) OD $\perp$ BC;
b) Điểm F cách đều ba cạnh của tam giác ABE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 3 2020
a) Ta có: AIBC nội tiếp ( O')
=> ^BAC = ^BIC (1)
ABDE nội tiếp ( O) có CA là tiếp tuyến
=> ^CAB = ^ADB ( cùng chắn cung AB ) (2)
Từ (1) ; (2) => ^ADB = ^BIC => ^KDB = ^CIB => B; I; K; D nội tiếp => ^KBD = ^KID
mà ^KBD = ^EBD = ^EAD = FAD
=> ^FAD = ^KID = ^FID
=> FAID nội tiếp
b) Kéo dài tia FD ------> tia Fx
FAID nội tiếp => ^DFI = ^DAI
I; A: C; B nội tiếp ( O') => ^IAB = ^ICB
=> ^DFI + ^ICB = ^DAI + ^IAB
Mà ^xDC = ^DFC + ^DCF = ^DFI + ^ICB
^DAB = ^DAI + ^IAB
=> ^xDC = ^DAB => ^xDB = ^DAB
=> Dx là tiếp tuyến ( O)
=> DF là tiếp tuyến ( O)
CM
11 tháng 4 2019
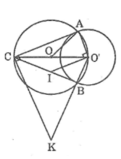
Trong đường tròn (O’) ta có AC và BC là hai tiếp tuyến cắt nhau tại C
Suy ra: 
(tính chất hai tiếp tuyến cắt nhau)
Mà O’I ⊥ O’A (gt)
CA ⊥ O’A (chứng minh trên)
Suy ra: O’I // CA => 
(hai góc so le trong)
Suy ra: 
Hay tam giác CIO’ cân tại I => IC = IO’
Khi đó I nằm trên đường trung trực của O’C
Lại có: 
(tính chất hai tiếp tuyến cắt nhau)
KC ⊥ CA (gt)
O’A ⊥ AC (chứng minh trên)
Suy ra: KC // O’A => 
(hai góc so le trong)
Suy ra: 
Hay tam giác CKO’ cân tại K => KC = KO’
Khi đó K nằm trên đường trung trực của O’C
Mặt khác: OC = OO’ (= R)
Suy ra O, I, K nằm trên đường trung trực của O’C
Vậy O, I, K thẳng hàng.
a) Có góc BAD =BOD ( vì cùng chắn cung BD) (*)
Lại có BAD cũng là góc nt chắn cung BC và góc BOC là góc ở tâm chắn cung BC
=> BAC =1/2 BOC
Từ (*) => BOD=1/2 BOC
=> BOD =COD ( vì cùng =1/2 BOC )
=>OD là tia p/g của góc BOC
mà tam giác BOC cân tại O
=> OD là tia p/g đồng thời cũng là đường cao của tam giác BOC
=> OD vuông góc BD (đpcm)
a)Xét đt O có :
ΔOBC cân tại O (OB=OC bk đt O)
Có góc BOD chắn cung BD
Mà góc BAD cùng chắn cung BD
⇒góc BOD=góc BAD=góc BAC
Má góc BAC chắn cung BC
⇒BAC=\(\dfrac{1}{2}\)cung BC
mà BOC = cung BC (cung chắn tâm)
⇒BOD=BAC=\(\dfrac{1}{2}\)BOD
b)Trong đt O',FAB=\(\dfrac{1}{2}\)FOB(góc nội tiếp=nửa góc ở tâm cùng chắn một cung)
Có EAB=EOB(cùng chắn cung EB)
⇒FAB=\(\dfrac{1}{2}\)EAB⇒AF là p|g EAB
cmtt⇒BF là p|g EBA
⇒F LÀ GIAO 3 ĐƯỜNG P|G EAB
⇒ Điểm F cách đều ba cạnh của tam giác ABE